Let A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.Solution in Tamil
The range of A(k) is [10√53,∞)
The range of A(k) is [20√53,∞)
If function k→A(k) is defined for k∈[−2,∞), then A(k) is many-one function
The value of k for which area is minimum is 1
The correct Answer is:B, C
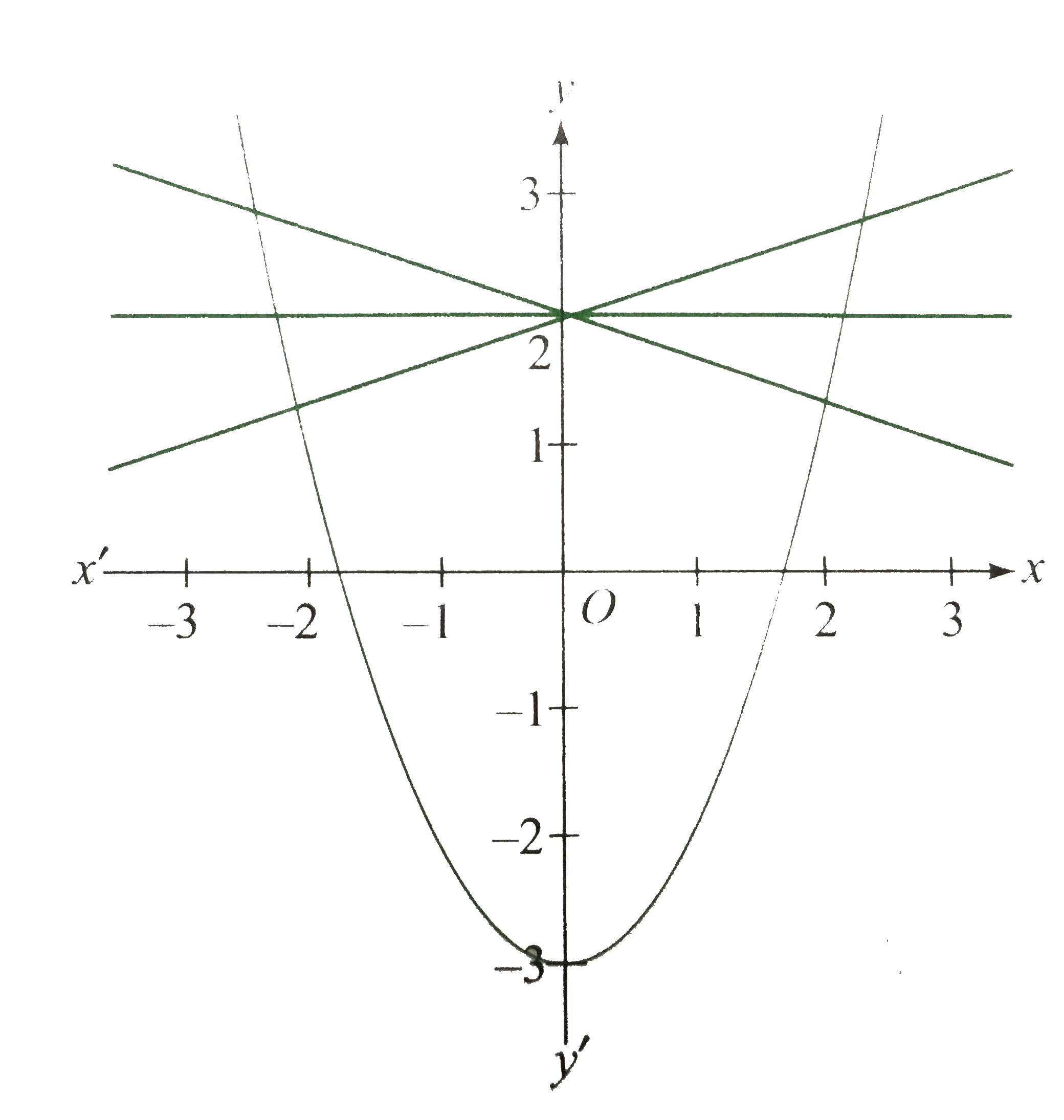
Line y=kx+2 passes through fixed point (0,2) for different value of k.
Also, it is obvious that minimum A(k) occurs when k=0, as when line is rotated from this position about point (0,2), the increased part of area is more than the decreased part of area. Therefore,
Minimum area =2√5∫0(2−(x2−3))dx
=2√5∫0(5−x2)dx
=2[5x−x33]√50
=2[5√5−5√53]
=20√53 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Single)
40 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Let Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio
View SolutionMatch the following lists :

View SolutionArea enclosed by the curve y=f(x) defined parametrically as x=1−t21+t2,y=2t1+t2isequa<o πsq.units (b) π2sq.units 3π4sq.units (d) 3π2sq.units
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionLet A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionConsider the ellipse x2f(k2+2k+5)+y2f(k+11)=1. If f(x) is a positive decr4easing function, then the set of values of k for which the major axis is the x-axis is (−3,2). the set of values of k for which the major axis is the y-axis is (−∞,2). the set of values of k for which the major axis is the y-axis is (−∞,−3)∪(2,∞) the set of values of k for which the major axis is the y-axis is (−3,−∞,)
View SolutionThe equation ∣∣∣√x2+(y−1)2−√x2+(y+1)2∣∣∣=K will represent a hyperbola for K∈(0,2) (b) K∈(−2,1) K∈(1,∞) (d) K∈(0,∞)
View SolutionIf the function f(x)=x2−kx+5 is increasing on [2, 4] , then (a) k∈(2, ∞) (b) k∈(−∞, 2) (c) k∈(4, ∞) (d) k∈(−∞, 4)
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+2=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+2=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionLet A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionConsider the ellipse x2f(k2+2k+5)+y2f(k+11)=1. If f(x) is a positive decr4easing function, then the set of values of k for which the major axis is the x-axis is (−3,2). the set of values of k for which the major axis is the y-axis is (−∞,2). the set of values of k for which the major axis is the y-axis is (−∞,−3)∪(2,∞) the set of values of k for which the major axis is the y-axis is (−3,−∞,)
View SolutionThe equation ∣∣∣√x2+(y−1)2−√x2+(y+1)2∣∣∣=K will represent a hyperbola for (a)K∈(0,2) (b) K∈(−2,1) K∈(1,∞) (d) K∈(0,∞)
View SolutionLet A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View Solution
