Which of the following have the same bounded area f(x)=s∈x,g(x)=sin2x,where0≤x≤10π f(x)=s∈x,g(x)=|s∈x|,where0≤x≤20π f(x)=|s∈x|,g(x)=sin3x,where0≤x≤10π f(x)=s∈x,g(x)=sin4x,where0≤x≤10π
f(x)=sinx,g(x)=sin2x, where 0≤x≤10π
f(x)=sinx,g(x)=|sin|, where 0≤x≤20π
f(x)=|sin|,g(x)=sin3x, where 0≤x≤10π
f(x)=sinx,g(x)=sin4x, where 0≤x≤10π
The correct Answer is:A, C, D
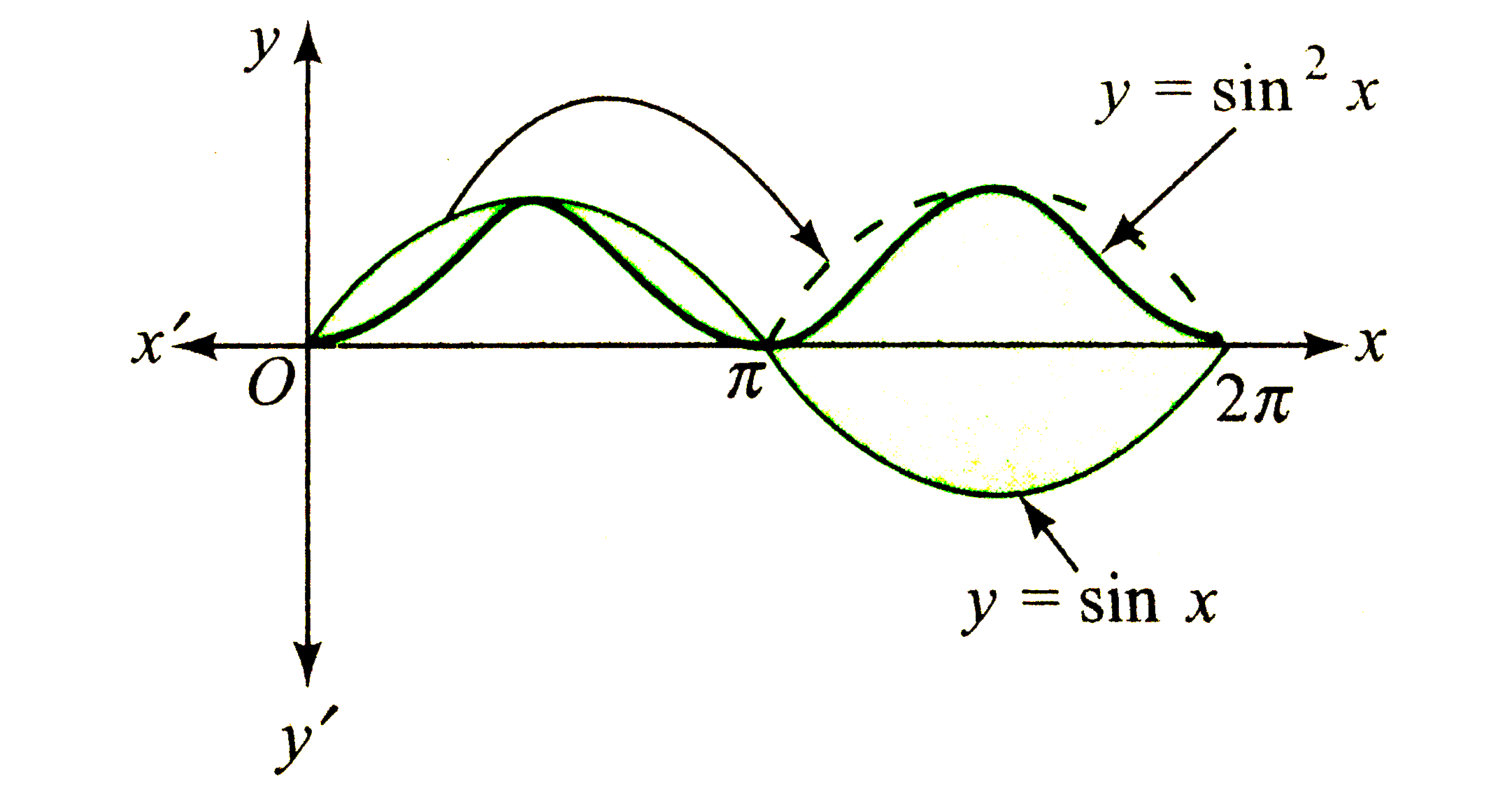
We know that area bounded by y=sinx and x-axis for x∈[0,π] is 2 sq. units.
Then area bounded by y=sinxandy=sin2x is 4 sq. units for x∈[0,2π].
Then for x∈[0,10π], the area bounded is 20 sq. units.

The area bounded by y= sin x and y = |sinx| for x∈[0,2π] is 4 sq. units.
Then for x∈[0,20π], the area bounded is 40 sq. units.
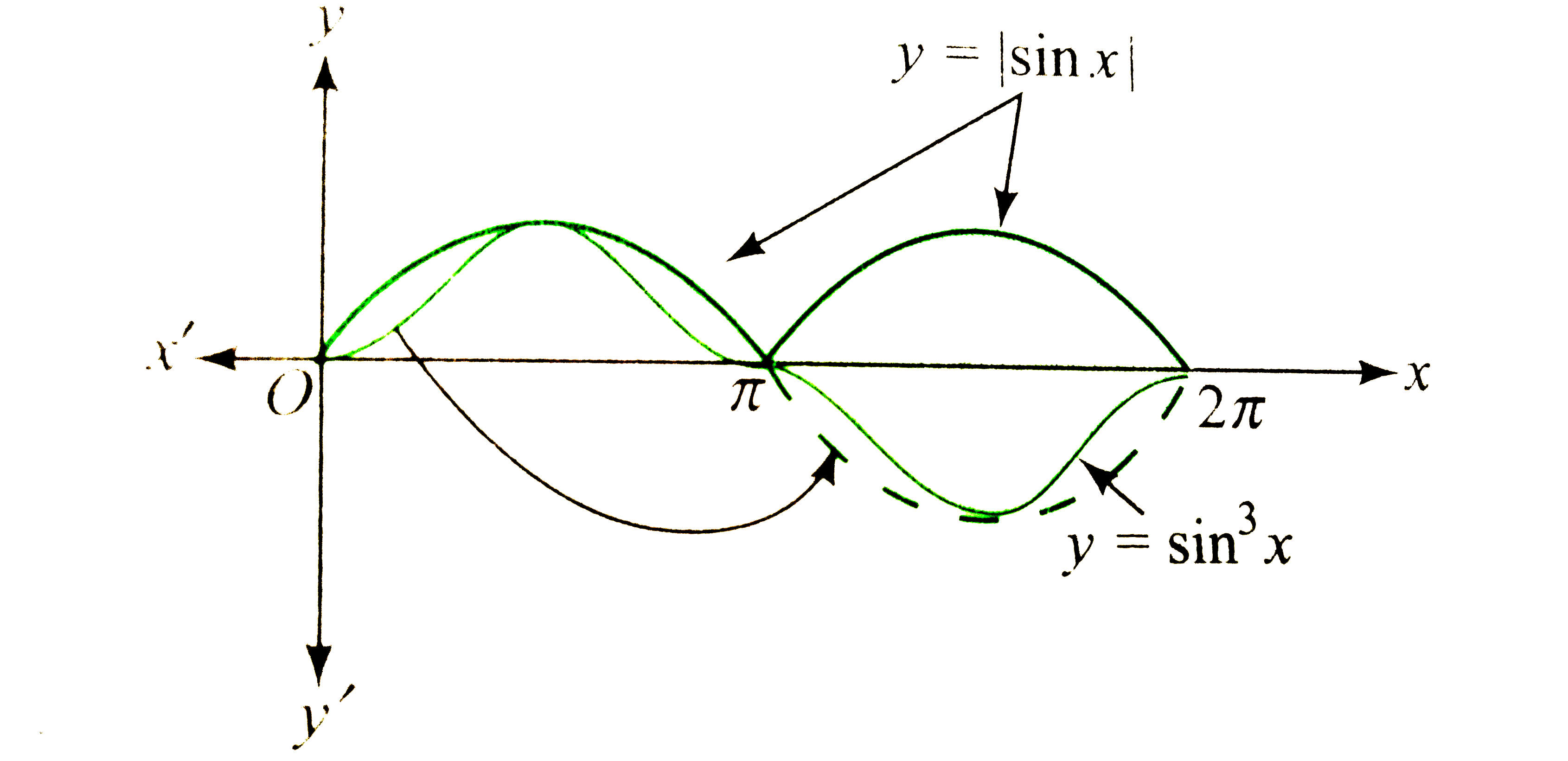
The area bounded by y=sinxandy=sin3x for x∈[0,2π] is 4 sq units.
Then for x∈[0,10π], the area bounded is 20 sq. units. Similarly, the area bounded by y=sinxandy=sin4x for x∈[0,10π] is 20 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Single)
40 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Knowledge Check
If f(x)=sinxex in [0,π] then f(x)
Asatisfies Rolle's theorem and c=π4 so that f'(π4)=4Bdoes not satisfy Rolle's theorem but f'(π4)>0Csatisfies Rolle's theorem and f'(π4)=0Dsatisfies Lagrange's Mean Value theorem but f'(π4)≠0
Solve for xandy:√3sinx+cosx=8y−y2−18,where0≤x≤4π,y∈R
View SolutionIf f(x)=xsinx and g(x)=xtanx,where 0<x≤1, then in this interval
View SolutionDiscuss monotonocity of f(x)=xsinxand g(x)=xtanx,where<x≤1
View SolutionFind the area of the region bounded by the x-axis and the curves defined by y=tanx(where−π3≤x≤π3) and y=cotx(whereπ6≤x≤3x2) .
View SolutionFind the area of the region bounded by the x-axis and the curves defined by y=tanx(where−π3≤x≤π3) and y=cotx(whereπ6≤x≤3x2) .
View SolutionEvaluate the following integral: ∫90f(x)dx, where f(x)=sinx, 0≤x≤π/2<br>
where f(x)=1,π2≤x≤3
where f(x)=ex−3, 3≤x≤9
View SolutionWrithe the range of the function f(x)=cos[x], where− π2<x<π2.
View Solution
