The area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis isSolution in Tamil
3
6
9
12
The correct Answer is:C
The given parabola is (y−2)2=x−1. So
dydx=12(y−2)
At(2,3),
dydx=12(3−2)=12
Tangent at (2,3) is
y−3=12(x−2)⇒x−2y+4=0
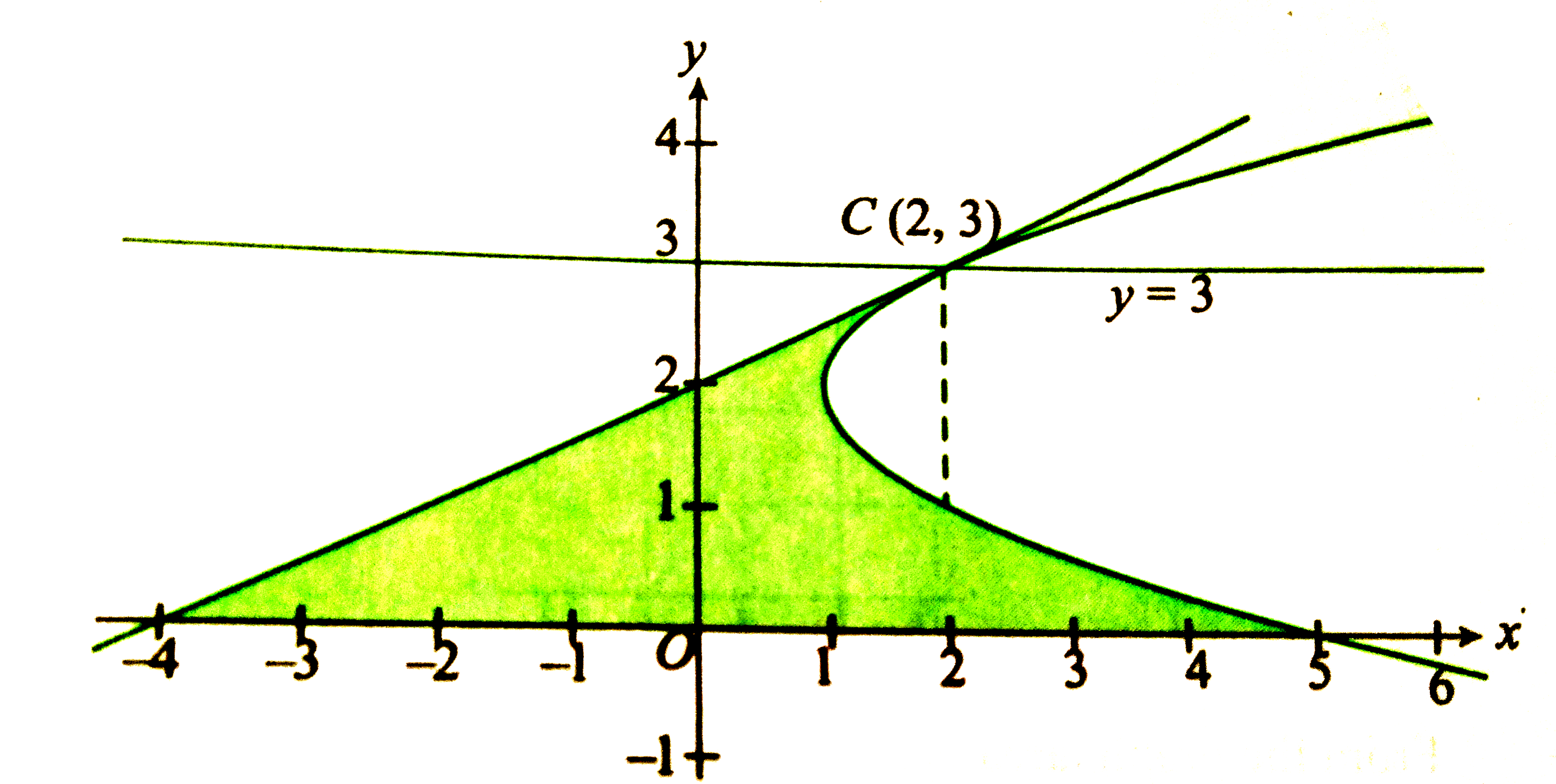
Therefore, the required area
=3∫0[(y−2)2+1]dy−3∫0(2y−4)dy
=∣∣
∣∣(y−2)33+y∣∣
∣∣30−∣∣y2−4y∣∣30
=13+3+83−(9−12)
=9 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Single Correct Answer Type
27 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)
16 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area bounded by the curves x+2|y|=1 and x=0.
View SolutionThe area enclosed between the curve y=sin2xandy=cos2x in the interval 0≤x≤π is _____ sq. units.
View SolutionThe area enclosed by the curve C:y=x√9−x2(x≥0) and the x-axis is___.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionFind the area of the figure bounded by parabola y=−x2−2x+3, the tangent to it at the point (2−5) and the y-axis.
View SolutionThe area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the x-axis is
View SolutionThe area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the x-axis is
View SolutionThe area of the figure bounded by the parabola (y−2)2 =x-1 , the tangent to it at the point with ordinate 3 and the x-axis is :
View SolutionThe area of the region bounded by the parabola (y−2)2=x−1 , the tangent to the parabola at the point (2,3) and the x-axis is :
View SolutionThe area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the x-axis is
View SolutionThe area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
View SolutionFind the area bounded by the parabola y=x2−2x+2, the line tangent to it at the point M(3,5) and the axis of ordinates
View SolutionThe area of the region bounded by the parabola (y−2)2=x−1,
the tangent to the parabola at the point (2,3) and the x-axis is
View Solutionपरवलय (y−2)2=x−1, परवलय की बिन्दु (2,3) पर स्पर्श रेखा और x-अक्ष द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है -
View SolutionThe area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the x-axis is
View Solution
