The area (in sq units) of the region {(x,y):y2≥2xandx2+y2≤4x,x≥0,y≥0} isSolution in Tamil
π−83
π−4√23
π2−2√23
π−43
The correct Answer is:A
y2=2xandx2+y2=4x meet at O(0,0)andB(2,2){(2,−2) is not considered as x,y≥0}
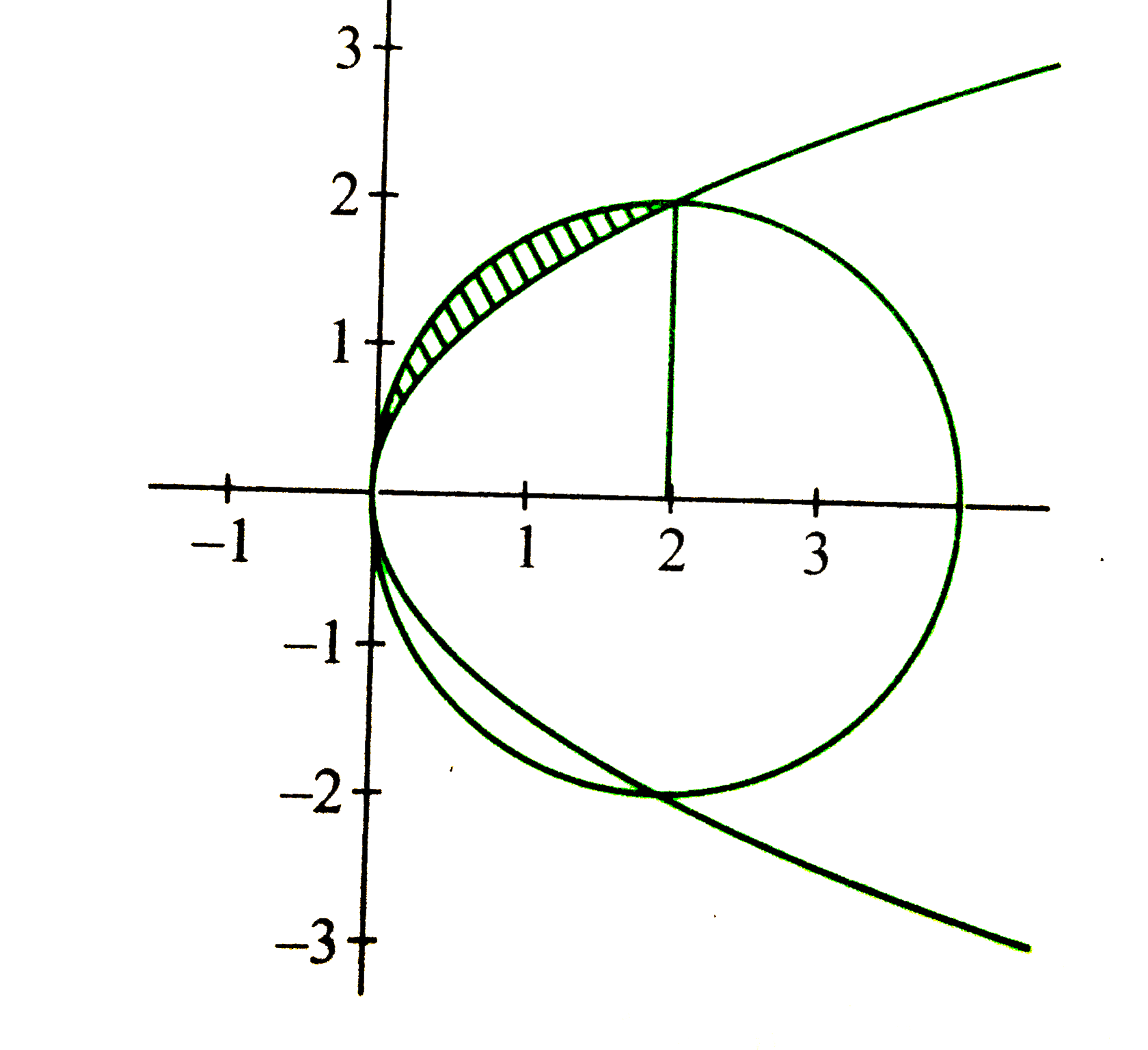
Now required area =14π×4−2∫0√2xdx
=π−√223[x3/2]20
=π−83
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year9videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Single Correct Answer Type27videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)16videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Find the area bounded by the curves x+2|y|=1 and x=0.
05:15View SolutionThe area enclosed between the curve y=sin2xandy=cos2x in the interval 0≤x≤π is _____ sq. units.
03:59View SolutionThe area enclosed by the curve C:y=x√9−x2(x≥0) and the x-axis is___.
09:00View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
01:25View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
05:50View Solutionif sqrt (x ^ (2) + y ^ (2)) = ae ^ (tan ^ (- 1) ((y) / (x))), a> 0, (y (0)> 0) then y (0) equals
05:44View SolutionThe area (in sq units) of the region {(x,y):y^(2)>=2x and x^(2)+y^(2) =0,y>=0} is
06:48View SolutionFind the area bounded by (x−y)(x+y)=1 and x2+y2=4,x>0,y>0.
03:19View SolutionThe area (in sq. units) of the region described by A={(x,y):y≥x2−5x+4,x+y>1,y≤0} is
04:21View SolutionThe area of the region for which o<y<3−2x−x2 and x>0, is
03:45View Solution12x +3y का अधिकतम मान जबकिx+y≤5,4x+y≤9,x≥0,y>0 हैं,
04:06View SolutionFind the area of the region {(x,y):x2+y2<1<x+y}
(ii) Find the area of the region {(x,y):x2+y2<2ax,y2>ax,x>0,y>0}
(iii) Using integration find the area of the region {x,y):y2<4x,4x2+4y2<9}.11:47View SolutionDomain and range of the realtion R={(x,y) : [x]+[y]=2, x gt 0, y gt 0} are
02:48View Solutionthe area of region for which 0<y<3−2x−x2 and x>0 is
04:46View SolutionThe area (in sq units) of the region {(x,y):y2≥2xandx2+y2≤4x,x≥0,y≥0} is
View Solution

