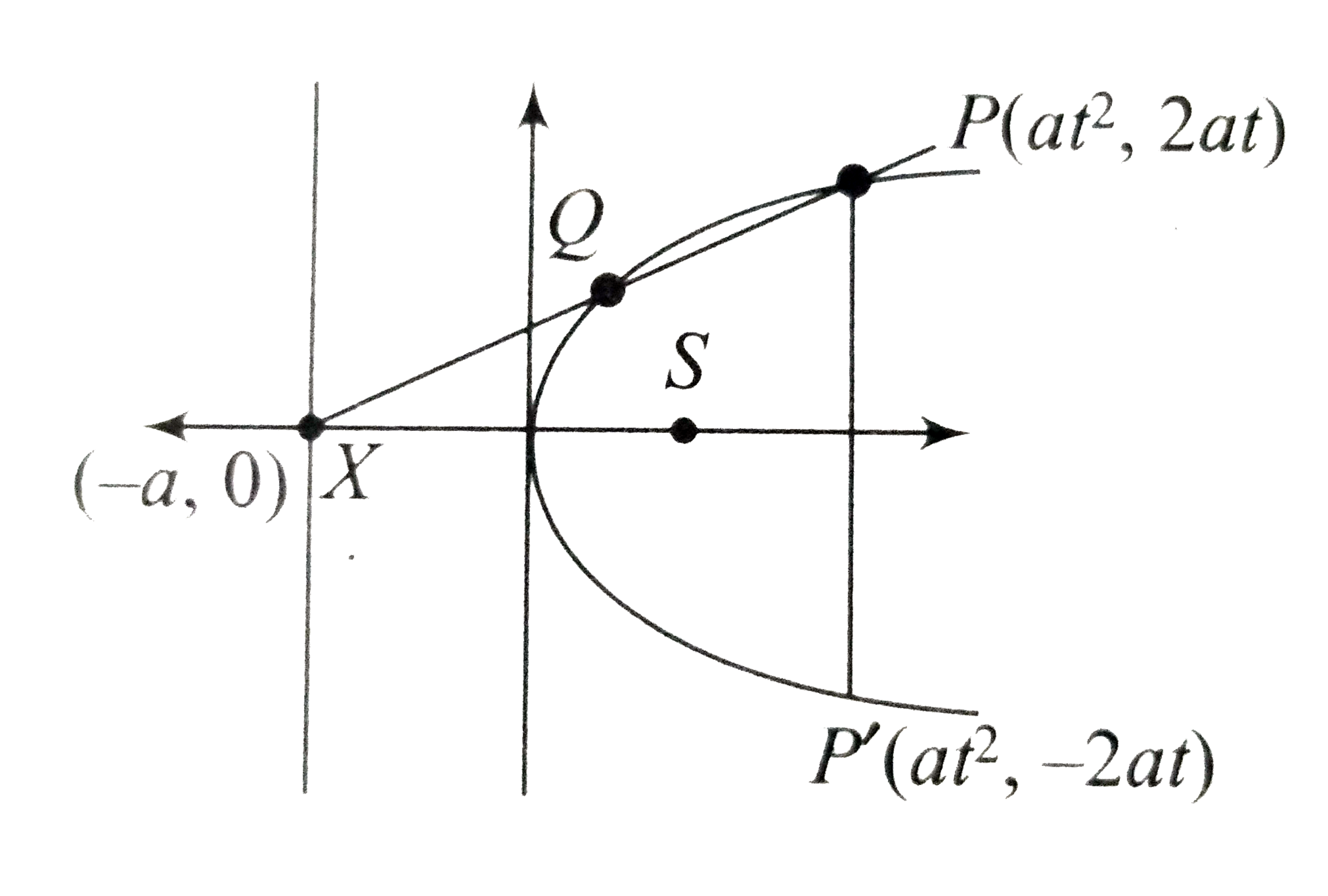
If X is the foot of the directrix on the a parabola. PP' is a double ordinate of the curve and PX meets the curve again in Q. Then prove that P' Q passes through the focus of the parabola.Solution in Tamil

A

line

B

circle

C

parabola

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$X : (- a, 0)$
$P X : y = \frac{2 a t - 0}{a t^{2} + a} (x + a)$
or $(1 + t^{2}) y = 2 t (x + a)$
Solving with parabola $y^{2} = 4 a x$ , we get
$\frac{4 t^{2} {(x + a)}^{2}}{{(1 + t^{2})}^{2}} = 4 a x$
or $t^{2} {(x + a)}^{2} = a x {(1 + t^{2})}^{2}$
or $t^{2} x^{2} - (a + a t^{4}) x + a t^{2} = 0$
or $x t^{2} (x - a t^{2}) - a (x - a t^{2}) = 0$
or $x = \frac{a}{t^{2}}$
$∴ Q : (\frac{a}{t^{2}}, \frac{2 a}{t})$
Thus $P' (a t^{2} - 2 a t)$ and $Q (\frac{a}{t^{2}}, \frac{2 a}{t})$ , are extremities of focal chord.
So, tangents at P' and Q intersect on directrix.

|

Updated on:21/07/2023

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

CENGAGE-PARABOLA-Single Correct Answer Type

Home
Ask Doubt
Profile