$P C$ is the normal at P to the parabola $y^{2} = 4 a x, C$ being on the axis. $C P$ is produced outwards to disothat $P Q = C P$ ; show that the locus of Q is a parabola.

A

$(a, 0)$

B

$(- a, 0)$

C

$(- 2 a, 0)$

D

$(2 a, 0)$

Text Solution

Verified by Experts

The correct Answer is:D

For parabola $y^{2} = 4 a x$ , normal at $P (a t^{2}, 2 a t)$ is $y = - t x + 2 a t + a t^{3}$

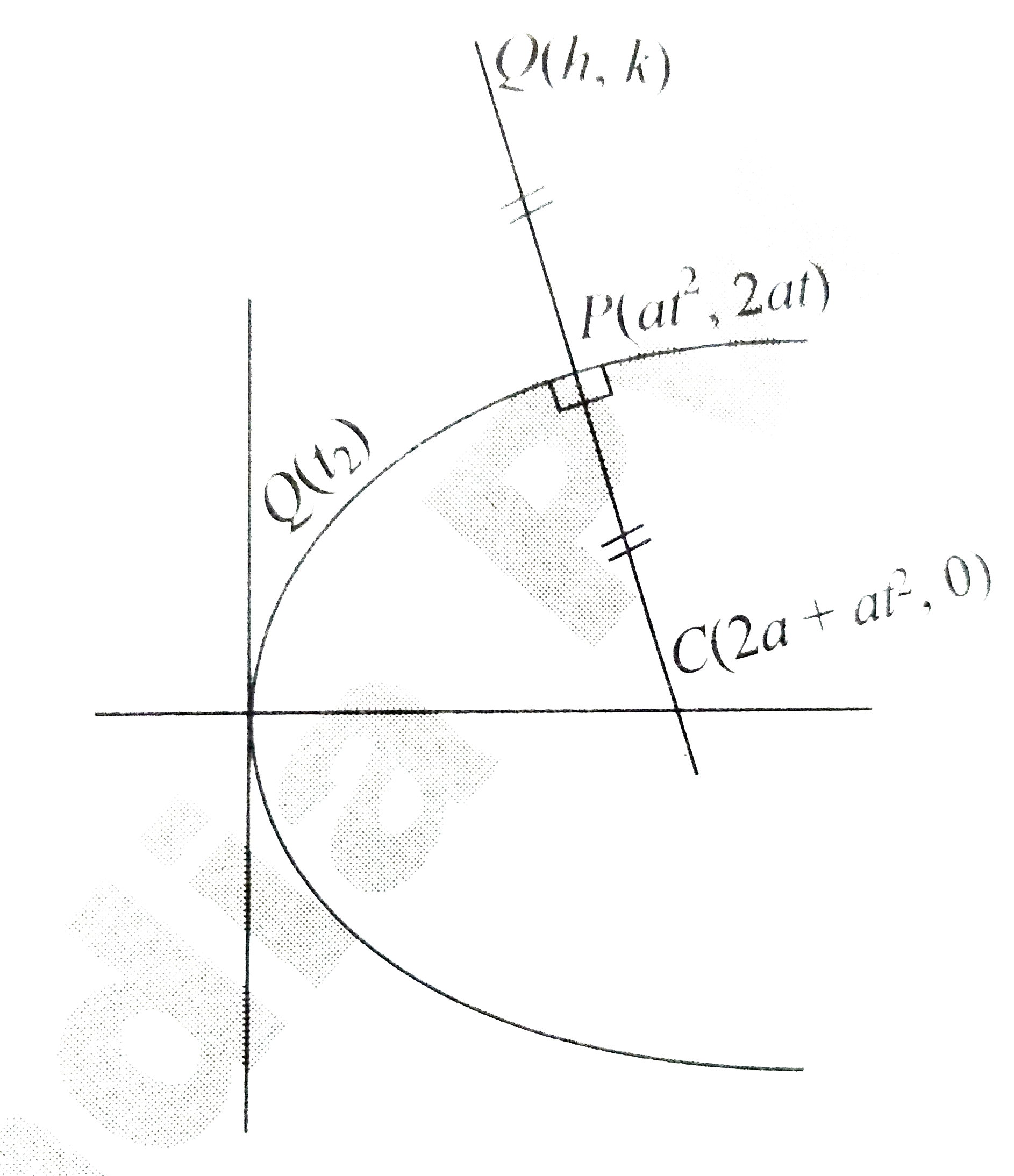
Putting $y = 0$ , we get
$t x = 2 a t + a t^{3}$
$\Rightarrow x = 2 a + a t^{2} = a (2 + t^{2})$
$∴ C \equiv (2 a + a t^{2}, 0)$
Since, $P Q = C P, P$ is the mid point of QC.
$∴ h + 2 a + a t^{2} = 2 a t^{2}$ (i)
and $k = 4 a t$
$\Rightarrow t = k / 4 a$
Putting value of t in (i), we get
$h + 2 a = a {(\frac{k}{4 a})}^{2}$
$\Rightarrow h + 2 a = \frac{k^{2}}{16 a}$
$\Rightarrow y^{2} = 16 a (x + 2 a)$
which has focus at $(2 a, 0)$ .

Updated on:21/07/2023

|

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Normal at a point P on the parabola $y^{2} = 4 a x$ meets the axis at Q such that the distacne of Q from the focus of the parabola is 10a. The coordinates of P are :
A $(6 a, 9 a)$
B $(6 a, - 9 a)$
C $(9 a, 6 a)$
D $(3 a, 6 a)$

CENGAGE-PARABOLA-Single Correct Answer Type

Home
Ask Doubt
Profile