If the normal at a point P to the hyperbola meets the transverse axis at G, and the value of SG/SP is 6, then the eccentricity of the hyperbola is (where S is focus of the hyperbola)Solution in Tamil
2
4
6
8
The correct Answer is:C
Equation of normal at point P(asecθ,btanθ) on hyperbola x2a2−y2b2=1 is
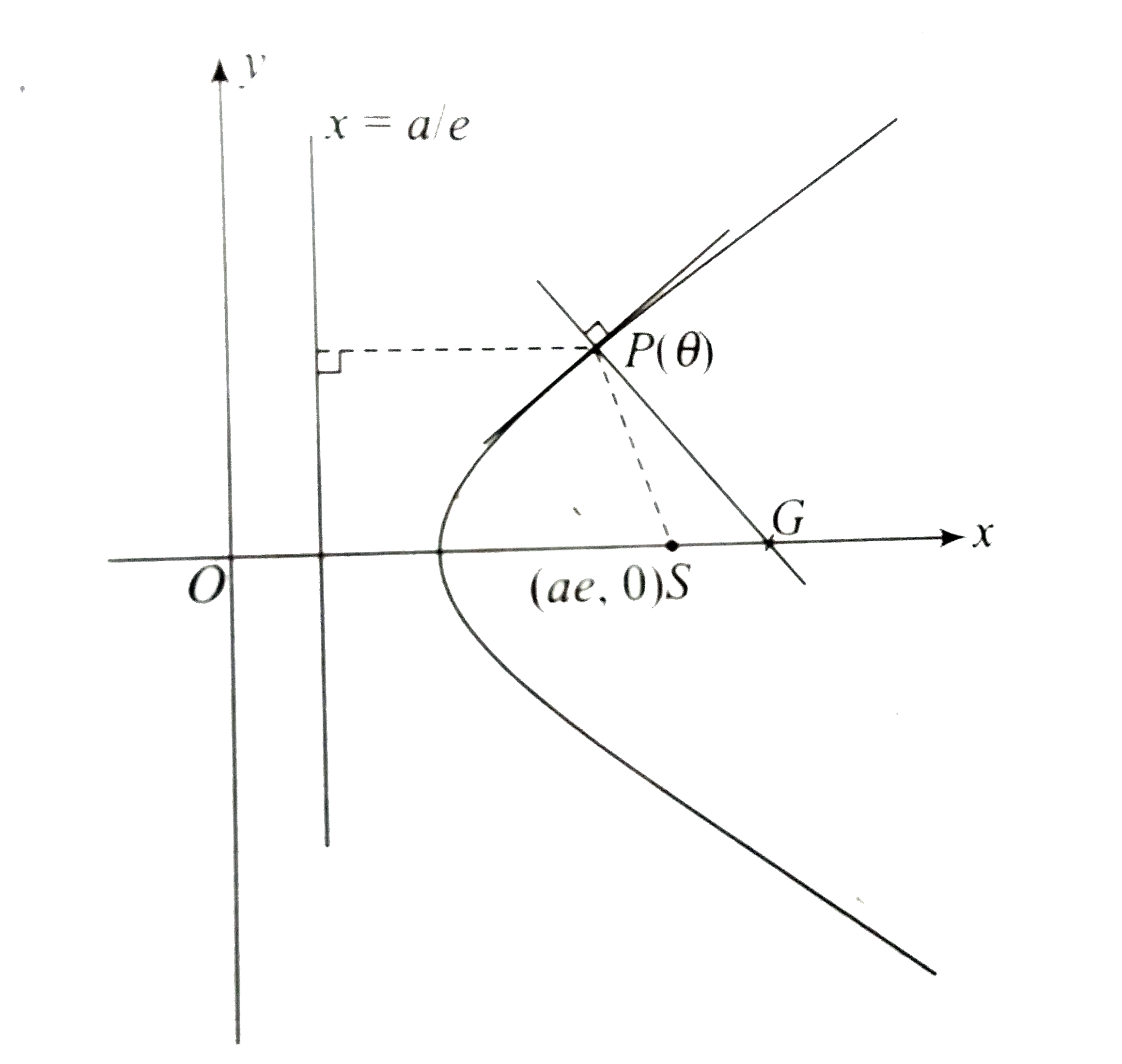
acosθx+bcotθy=a20+b2
∴G(a2+b2acosθ,0)
S(ae,0)
SP=e(asecθ)−a
Also SG=a2+b2acosθ−ae=a2e2acosθ−ae=e[e(asecθ)−a]
⇒SG/SP=e=6
Similar Questions
Normal to a rectangular hyperbola at P meets the transverse axis at N. If foci of hyperbola are S and S', then find the value of SNSP.
View SolutionIf the normal at a pont P to the hyperbola x2a2−y2b2=1 meets the x-axis at G, show that the SG=eSP.S being the focus of the hyperbola.
View SolutionIf asymptotes of hyperbola bisect the angles between the transverse axis and conjugate axis of hyperbola, then what is eccentricity of hyperbola?
View SolutionIf the normal at a point P to the hyperbola meets the transverse axis at G, and the value of SG/SP is 6, then the eccentricity of the hyperbola is (where S is focus of the hyperbola)
View SolutionFor the hyperbola x2a2+y2b2=1, the normal at point P meets the transverse axis AA' in G and the connjugate axis BB' in g and CF be perpendicular to the normal from the centre. Q. Locus of middle-point of G and g is a hyperbola of eccentricity
View SolutionNormal to a rectangular hyperbola at P meets the transverse axis at N. If foci of hyperbola are S and S', then find the value of SNSP.
View SolutionIf the normal at a pont P to the hyperbola x2a2−y2b2=1 meets the x-axis at G, show that the SG=eSP.S being the focus of the hyperbola.
View SolutionIf asymptotes of hyperbola bisect the angles between the transverse axis and conjugate axis of hyperbola, then what is eccentricity of hyperbola?
View Solution
