A circle x2+y2=a2 meets the x-axis at A(-a,0) and B(a,0). P(α) and Q(β) are two points on the circle so that α−β=2γ, where γ is a constant. Find the locus of the point of intersection of AP and BQ.Solution in Tamil
Let
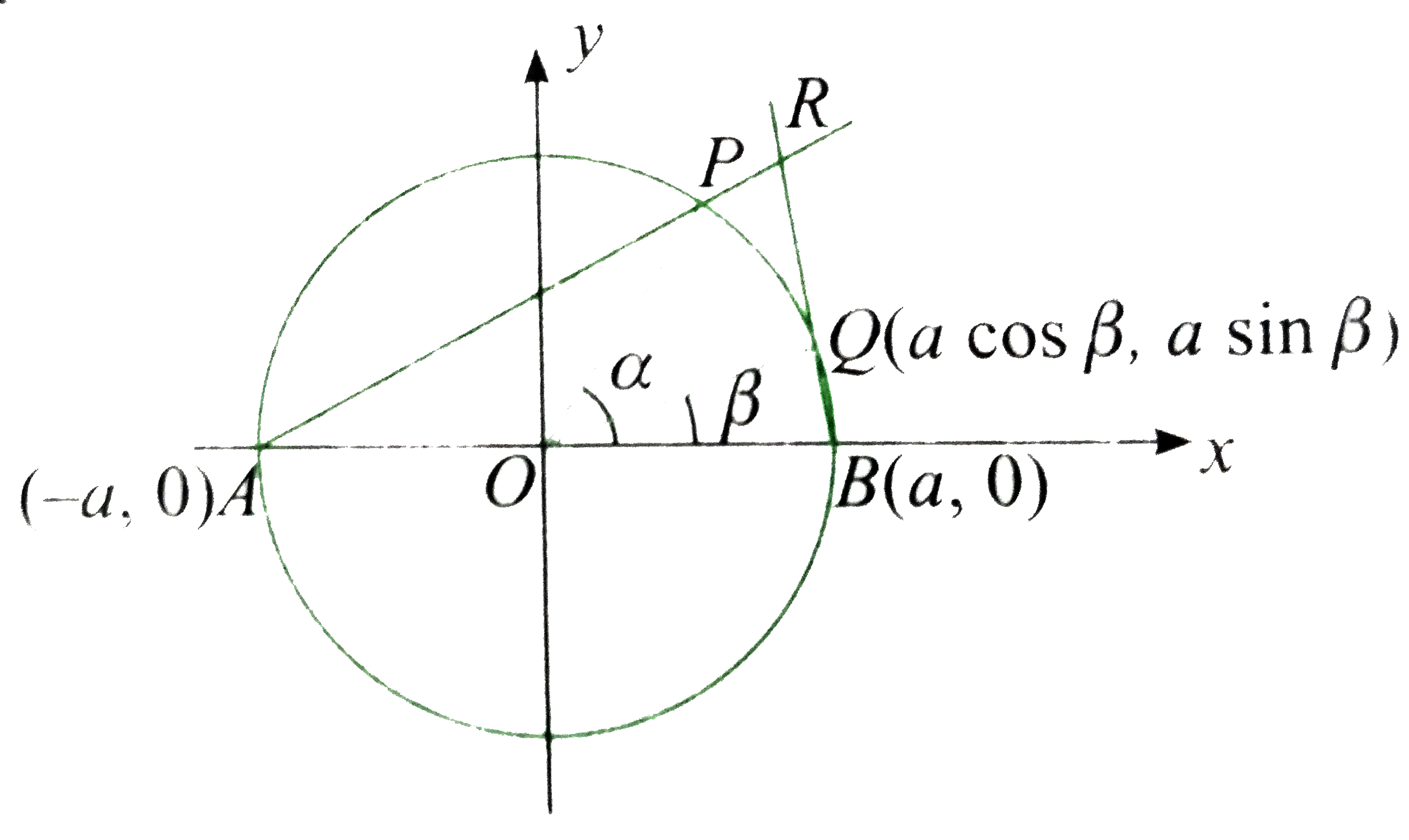
The coordinates of A are ( -a,0) and that of P are (acosα,asinα).
Therefore, the equation of AP is
y=asinαa(cosα+1)(x+a)
or y=tan.α2(x+a) (1)
Similarly, the equationof BQ is
y=asinβa(cosβ−1)(x−a)
or y=−cot.β2(x−a) (2)
We now eliminate α and β from (1) and (2). Therefore,
tan.α2=ya+x,tan.β2=a−xy
Now, α−β=2γ⇒γ=α2−β2
∴tanγ=tan.α2−tan.β21+tan.α2tan.β2=ya+x−a−xy1+ya+x.a−xy
or tanγ=y2−(a2−x2)(a+x)y+(a−x)y
=x2+y2−a22ay
or x2+y2−2aytanγ=a2
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
06:38View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
04:31View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is05:33View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
02:21View SolutionA circle with center at the origin and radius equal to a meets the axis of x at AandB.P(α) and Q(β) are two points on the circle so that α−β=2y , where γ is a constant. Find the locus of the point of intersection of AP and BQ.
04:35View Solutionif α,β,γ are non-constant terms in G.P. and equations αx2+2βx+γ=0 and x2+x−1=0 has a common root then (γ−α).β is
05:29View SolutionA circle x2+y2=a2 meets the x-axis at A(-a,0) and B(a,0). P(α) and Q(β) are two points on the circle so that α−β=2γ, where γ is a constant. Find the locus of the point of intersection of AP and BQ.
06:02View SolutionIf α,βandγ are the roots of the equation x3+px+q=0 (with p≠0andp≠0andq≠0), the value of the determinant
∣∣ ∣ ∣∣αβγβγαγαβ∣∣ ∣ ∣∣, is07:22View SolutionIf alpha, beta, gamma are the roots of x^(3) + ax^(2) + b = 0 , then the value of |(alpha,beta,gamma),(beta,gamma,alpha),(gamma,alpha,beta)| , is
02:58View SolutionIf α,β,γ are the roots of x3+x2+x+1=0 then (α−β)2+(β−γ)2+(γ−α)2 =
08:55View SolutionSuppose α,β,γ are the roots of x3+x2+x+2=0 then the value of (α+β−2γγ)(β+γ−2αα)(γ+α−2ββ)
06:38View SolutionThe circle x2+y2=4 ,cuts the line joining the points A(1,0),&B(3,4) in two points P& Q.Let BPPA=α>0&BQQA=β>0 .Then α+β
06:22View SolutionIf α,β,γ are the roots of ax3+bx2+cx+d=0 and ∣∣ ∣ ∣∣αβγβγαγαβ∣∣ ∣ ∣∣=0,α≠β≠γ then find the equation whose roots are α+β−γ,β+γ−α, and γ+α−β.
07:45View SolutionA circle with center at the origin and radius equal to a meets the axis of x at AandB.P(α) and Q(β) are two points on the circle so that α−β=2γ , where γ is a constant. Find the locus of the point of intersection of AP and BQ.
03:24View Solutionα,βandγ are parametric angles of three points P, Q and R respectively, on the circle x2+y2=1 and A is the point (-1, 0). If the lengths of the chords AP, AQ and AR are in GP, then cosα2,cosβ2andcosγ2 are in
07:32View Solution

