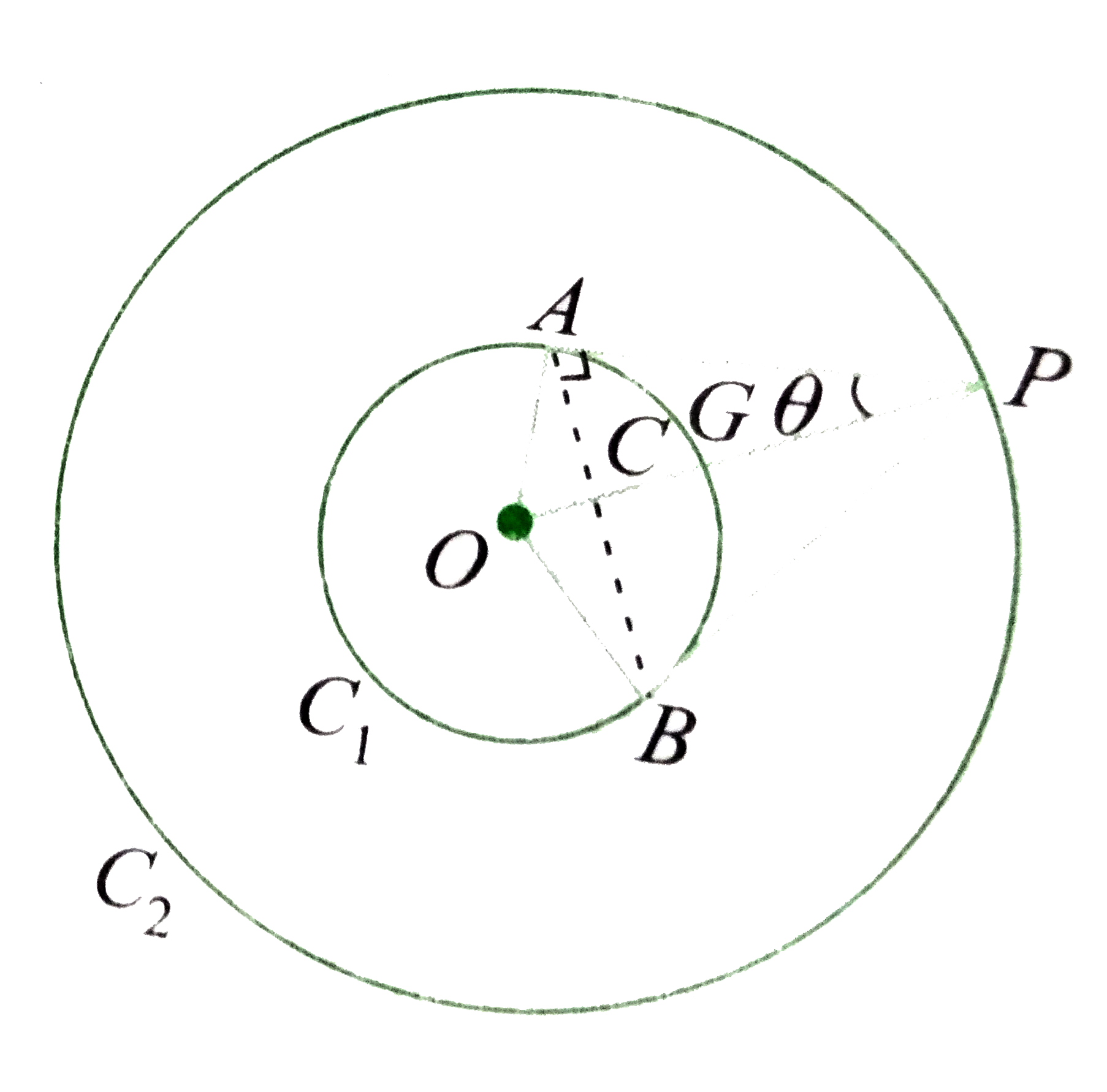
C1andC2 are two concentrate circles, the radius of C2 being twice that of C1. From a point P on C2 tangents PA and PB are drawn to C1. Prove that the centroid of the ΔPAB lies on C1Solution in Tamil
Let r be the radius of C1 and 2r be the radius of C2.Then, OA=OB=r
and OP=2r
Since PA and PB are tangents to C1,
∠OAP=∠OBP=90∘
Let OP meets C1 at G.
Let ∠OPA=θ. Then,
sinθ=OAOP=r2r=12
or θ=30∘
or ∠AOP=60∘
In ΔOAC,
cos60∘=OCOA
or 12=OCror OC=r2
∴PC=2r−r2−3r2
Also, CG=r−OC=r−r2=r2
Clearly, CG=13PC
Therefore, G is the centroid of ΔABP.
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
09:11View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
04:06View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is05:36View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
09:34View SolutionTransverse common tangents are drawn from O to the two circles C_(1),C_(2) with 4,2 respectively.Then the ratio of the areas of triangles formed by the tangents drawn from O to the circles C_(1) and C_(2) and chord of contacts of O w.r.t the circles C_(1) and C_(2) respectively is
10:25View SolutionProve that (C_(0)+C_(1))(C_(1)+C_(2))(C_(2)+C_(3))(C_(n-1)+C_(n))=((n+1)^(n))/(n!)*c_(0)*C_(1)*C_(2).........
03:26View SolutionIf C1:x2+y2=(3+2√2)2 be a circle. PA and PB are pair of tangents on C1 where P is any point on the director circle of C1, then the radius of the smallest circle which touches C1 externally and also the two tangents PA and PB is
07:06View SolutionEvaluate ∣∣ ∣∣mC1mC2mC3nC1nC2nC3pC1pC2pC3∣∣ ∣∣
02:53View SolutionC1andC2 are two concentrate circles, the radius of C2 being twice that of C1. From a point P on C2 tangents PA and PB are drawn to C1. Prove that the centroid of the ΔPAB lies on C1
09:20View SolutionIf C1,C2,C3,... is a sequence of circles such that Cn+1 is the director circle of Cn. If the radius of C1 is 'a', then the area bounded by the circles Cn and Cn+1, is
02:10View SolutionProve that : Prove that
C1C0+2.C2C1+3.C3C2+….+n.CnCn−1=n(n+1)203:35View SolutionIf C0,C1,C2,…,Cn are the binomial coefficients in the expansion of (1+x)n⋅n being even, then C0+(C0+C1)+(C0+C1+C2)+….+(C0+C1+C2+…+Cn−1) is equal to :
02:42View SolutionC_(1) And C_(2) There are two concentric circles C_(2) Radius of C_(1) Is twice the radius. C_(2) From a point P C_(1) PA and two tangents on PB Prove that the triangle is drawn PAB Center of C_(1) Is located at.
02:48View SolutionProve that :
2C1+3C1+4C1=3C2+4C2.07:20View SolutionIf C1:x2+y2=(3+2√2)2 be a circle. PA and PB are pair of tangents on C1 where P is any point on the director circle of C1, then the radius of the smallest circle which touches C1 externally and also the two tangents PA and PB is
08:12View SolutionC1andC2 are two concentrate circles, the radius of C2 being twice that of C1. From a point P on C2 tangents PA and PB are drawn to C1. Prove that the centroid of the ΔPAB lies on C1
04:28View Solution

