$C_{1} and C_{2}$ are two concentrate circles, the radius of $C_{2}$ being twice that of $C_{1}$ . From a point P on $C_{2}$ tangents PA and PB are drawn to $C_{1}$ . Prove that the centroid of the $Δ P A B$ lies on $C_{1}$

Video Solution

Text Solution

Verified by Experts

Let the coordinates of point P be $(2 r cos θ, 2 r sin θ)$
We have , OA = r, OP = 2r
Since, $Δ O A P$ is a right angled triangle.

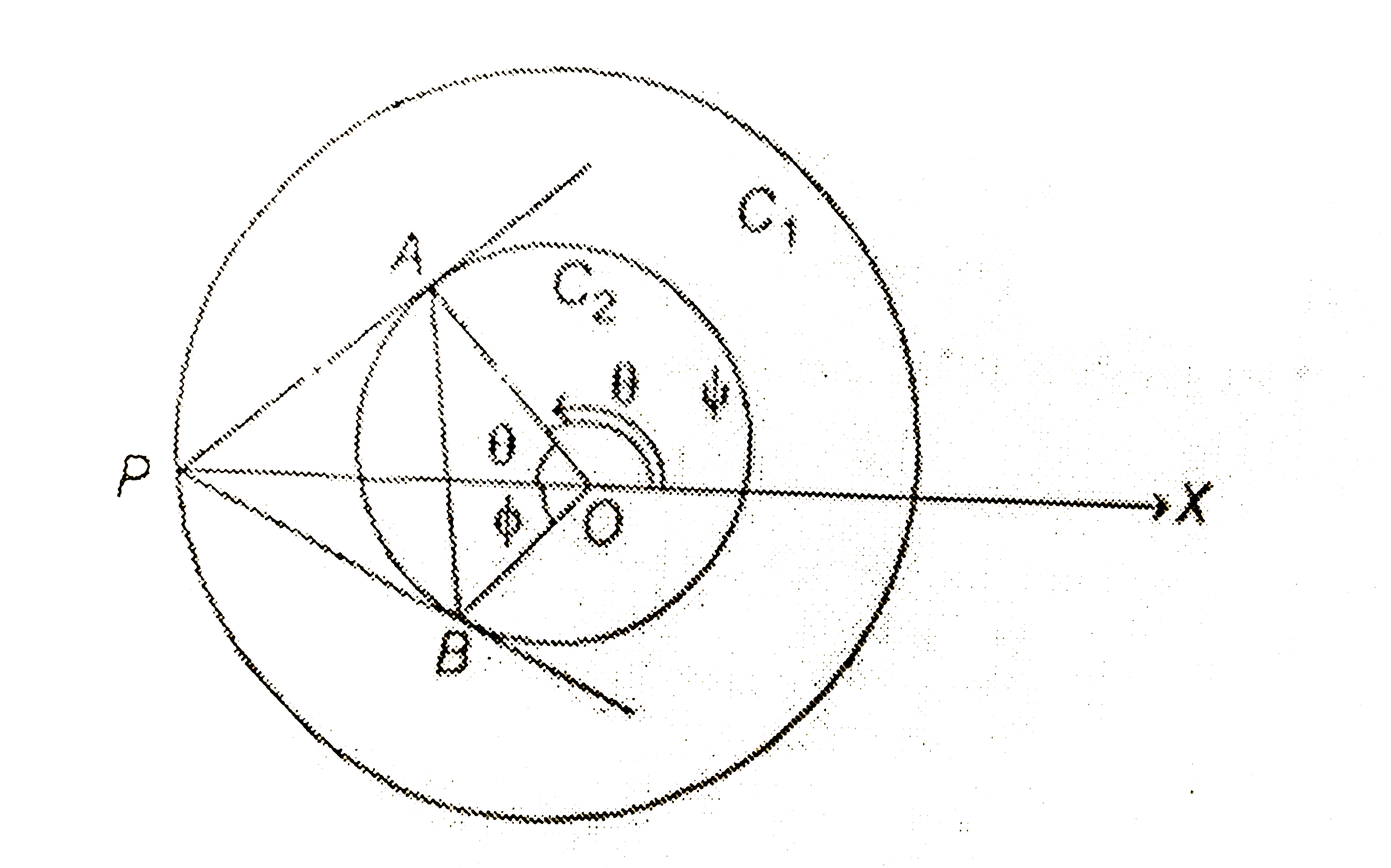
$cos ϕ = 1 / 2 \Rightarrow ϕ = π / 3$
$∴$ Coordinates of A are ${cos (θ - π / 3), r sin (θ - π / 3)}$
If p, q is the centroid of Delta PAB, then
$p = \frac{1}{3} [r cos (θ - π / 3) + r cos (θ + π / 3) + 2 r cos θ]$
$= \frac{1}{3} [r (2 cos \frac{θ - \frac{π}{3} + θ + \frac{π}{3}}{2} \cdot cos \frac{θ - \frac{π}{3} - θ - \frac{π}{3}}{2}) + 2 r cos θ]$
$\frac{1}{3} [r {2 cos θ π / 3} + 2 r cos θ]$
$= \frac{1}{3} [r \cdot cos θ + 2 r cos θ] = r cos θ$
and $q = \frac{1}{3} [r sin (θ - \frac{π}{3}) + r sin (θ + \frac{π}{3}) + 2 r sin θ]$
$= \frac{1}{3} [r (2 sin \frac{θ - \frac{π}{3} + θ + \frac{π}{3}}{2} \cdot cos \frac{θ - \frac{π}{3} - θ - \frac{π}{3}}{2}) + 2 r sin θ]$
$= \frac{1}{3} [r sin (2 sin θ cos π / 3) + 2 r sin θ]$
$= \frac{1}{3} [r (sin θ) + 2 r sin θ] = r sin θ$
Now, (p, q) = $(r cos θ, r sin θ) lies on x^{2} + y^{2} = r^{2}$ which is called $C_{1}$ .

Updated on:21/07/2023

$C_{1} and C_{2}$ are two concentric circles with centres at O. Their radii are 12 cm and 3 cm respectively. B and C are the points of contact of two tangents draw to $C_{2}$ from a point A lying on the circle $C_{1}$ . Then the area of the quadrilateral ABOC is-
A $\frac{9 \sqrt{15}}{2} c m^{2}$
B $12 \sqrt{15} c m^{2}$
C $9 \sqrt{15} c m^{2}$
D $6 \sqrt{15} c m^{2}$
$C_{1} and C_{2}$ are two concentric circles with centres at O. Their radii are 12 cm and 3 cm respectively. B is the point of contact of tangents drawn to $C_{2}$ from a point A lying on the circle $C_{1}$ . Then the area of the triangle OAB is :
A $\frac{9 \sqrt{15}}{2}$ sq. cm
B $12 \sqrt{15}$ sq. cm
C $9 \sqrt{15}$ sq. cm
D $6 \sqrt{15}$ sq. cm
Consider the circle $C_{1} : x^{2} + y^{2} - 6 x - 8 y + 15 = 0, C_{2} : x^{2} + y^{2} - 6 x - 8 y + 20 = 0$ Now from any point P on $C_{1},$ pair of tangents PA and PB are drawn on $C_{2} .$ Then locus of the orthocenter of triangle PAB is
A $x^{2} + y^{2} - 6 x - 8 y + 20 = 0$
B $x^{2} + y^{2} - 6 x - 8 y + 10 = 0$
C $x^{2} + y^{2} - 6 x - 8 y + 5 = 0$
Dnone of these