Two variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.Solution in Tamil
The correct Answer is:x2+y2=4r2
Let the point of intersection of tangents at A and be P≡(x,y) .
Since AB=AO=BO=r, we get
∠AOB=60∘
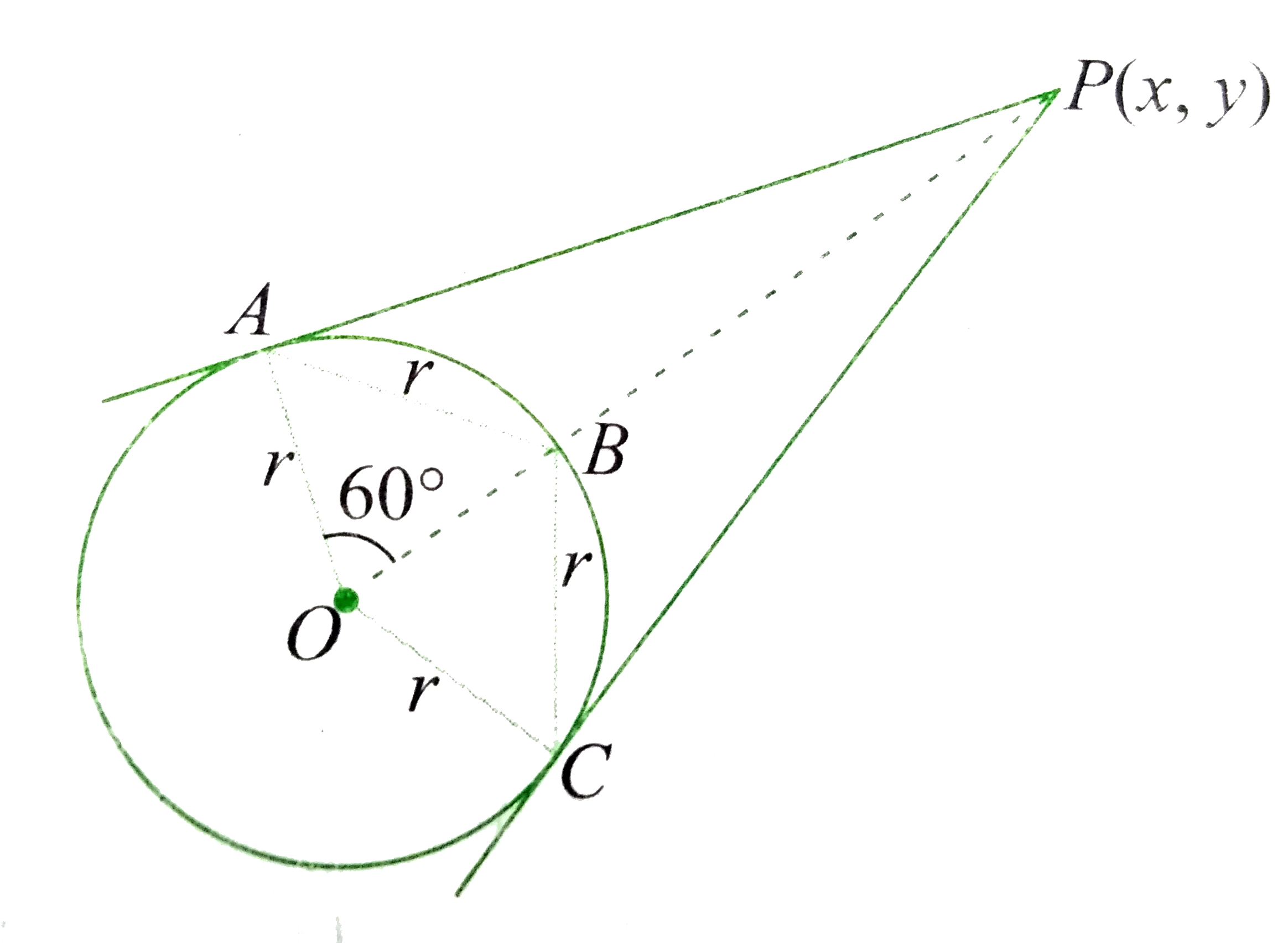
or PArtan60∘=√3
or √x2+y2−r2=√3r
Therefore, x2+y2=4r2 is the locus of the point P.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.414videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.512videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.25videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
Find the equation of the tangent to the circle x2+y2+4x−4y+4=0 which makes equal intercepts on the positive coordinates axes.
05:50View SolutionHow the following pair of circles are situated in the plane ? Als, find the number of common tangents . (i)x2+(y−1)2=9 and (x−1)2+y2=25 (ii) x2+y2−12x−12y=0 and x2+y2+6x+6y=0
03:18View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
02:55View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is04:07View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
03:51View SolutionTwo circles with centres AandB of radii 3cmand4cm respectively intersect at two points CandD such that ACandBC are tangents to the two circles. Find the length of the common chord CD.
04:41View SolutionThe tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
06:30View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
04:04View SolutionLet aandb be nonzero real numbers. Then the equation (ax2+by2+c)(x2−5xy+6y2)=0 represents. four straight lines, when c=0 and a,b are of the same sign. two straight lines and a circle, when a=b and c is of sign opposite to that a two straight lines and a hyperbola, when aandb are of the same sign and c is of sign opposite to that of a a circle and an ellipse, when aandb are of the same sign and c is of sign opposite to that of a
06:09View SolutionThe chords of contact of tangents from three points A,BandC to the circle x2+y2=a2 are concurrent. Then A,BandC will (a)be concyclic (b) be collinear (c)form the vertices of a triangle (d)none of these
02:12View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
01:35View SolutionIf the tangents to the parabola y2=4ax intersect the hyperbola x2a2−y2b2=1 at AandB , then find the locus of the point of intersection of the tangents at AandB.
02:59View SolutionLet aandb be nonzero real numbers. Then the equation (ax2+by2+c)(x2−5xy+6y2)=0 represents. four straight lines, when c=0 and a,b are of the same sign. two straight lines and a circle, when a=b and c is of sign opposite to that a two straight lines and a hyperbola, when aandb are of the same sign and c is of sign opposite to that of a a circle and an ellipse, when aandb are of the same sign and c is of sign opposite to that of a
06:43View SolutionTwo variable chords ABandBC of a circle x2+y2=r2 are such that AB=BC=r . Find the locus of the point of intersection of tangents at AandC.
04:40View SolutionThe chords of contact of tangents from three points A,BandC to the circle x2+y2=a2 are concurrent. Then A,BandC will be
03:56View SolutionTwo circles with centres AandB of radii 3cmand4cm respectively intersect at two points CandD such that ACandBC are tangents to the two circles. Find the length of the common chord CD.
03:39View Solution

