If the tangent at (3,−4) to the circle x2+y2−4x+2y−5=0 cuts the circle x2+y2+16x+2y+10=0 in A and B then the midpoint of AB is Solution in Tamil
The correct Answer is:(−6,−7)
Equation of tangent to circle x2+y2−4x+2y−5=0 at point (3,-4) is
3x−4y−2(x+3)=(y−4)−5=0
or x−3y−15=0 (1)
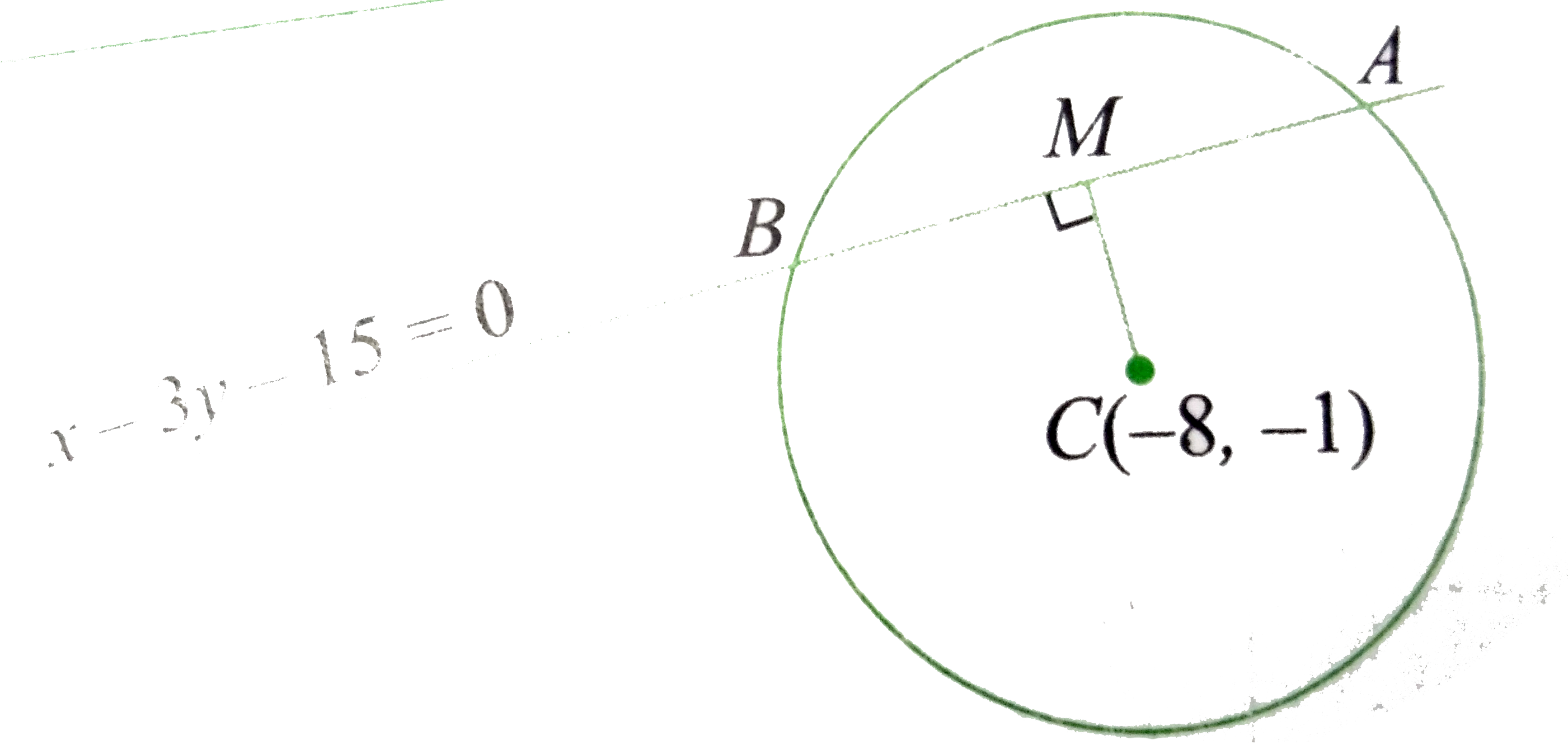
Center of the second circle is C(−8,−1).
Slope of CM is '−3'
Equation of CM is y+1=−3(x+8)
or 3x+y+25=0 (2)
Solving (1) and (2), we get M≡(−6,−7)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.512videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.318videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
How the following pair of circles are situated in the plane ? Als, find the number of common tangents . (i)x2+(y−1)2=9 and (x−1)2+y2=25 (ii) x2+y2−12x−12y=0 and x2+y2+6x+6y=0
06:12View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
00:59View SolutionFind the angle between the two tangents from the origin to the circle (x−7)2+(y+1)2=25
06:22View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is01:40View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
08:47View SolutionIf the tangent at (3,-4) to the circle x^(2)+y^(2)-4x+2y-5=0 cuts the circle x^(2)+y^(2)+16x+2y+10=0 in A and B then the midpoint of AB is
10:12View SolutionThe tangents to the circle x2+y2−4x+2y+k=0 at (1,1) is x−2y+1=0 then k=
05:04View Solutionरेखा x - y + 2 = 0 से वृत्त x2+y2+4x−2y=0 द्वारा कटे जीवा के मध्य बिन्दु के निर्देशांक ज्ञात कीजिए |
View SolutionThe centre of the circle x2+y2−4x−2y−4=0 is
03:32View SolutionIf the tangent at (3,-4) to the circle x2+y2−4x+2y−5=0 cuts the circle x2+y2+16x+2y+10=0 in A and B then the midpoint of AB is
08:47View SolutionThe equation of the tangent at the point (0, 3) on the circle which cuts the circles x2+y2−2x+6y=0,
x2+y2−4x−2y+6=0 and
x2+y2−12x+2y+3=0 orthogonally is06:27View SolutionIf the tangent at "(3,−4) to the circle x2+y2−4x+2y−5=0 cuts the circle x2+y2+16x+2y+10=0 in A and B then the midpoint of AB is
02:24View SolutionFind the equation of all common tangents of the circles
(i) x2+y2=9 and
x2+y(2)−16x+2y+49=0
(ii) x2+y2+4x+2y−4=0 and
x2+y2−4x−2y+4=004:57View SolutionThe tangent to the circle x2+y2−4x+2y+k=0 at (1,1) is x−2y+1=0 then k=
06:21View SolutionIf the tangent at (3,-4) to the circle x2+y2−4x+2y−5=0 cuts the circle x2+y2+16x+2y+10=0 in A and B then the midpoint of AB is
06:21View SolutionLocus of midpoints of chords of circles x2+y2−4x−2y−4=0 which are perpendicular to the line 4x−3y+10=0 is
04:22View Solution

