Question

about to only mathematics

Answer

75 sq. units

Explanation

The equation of the circle is
`x^(2)+y^(2)-2x-4y-20=0`
Center `-= (1,2) ` radius `=sqrt(1+4+20)=5`
The equation of tangent at `(1,7)` is
`x.1+y.7-(x+1)-2(y+7)-20=0`
or `y-7=0 ` (1)
Similarly, the equation of tangent at (4,-1) is
`4x-2y-(x+4)-2(y-2)-20=0`
or `3x-4y-20=0` (2)

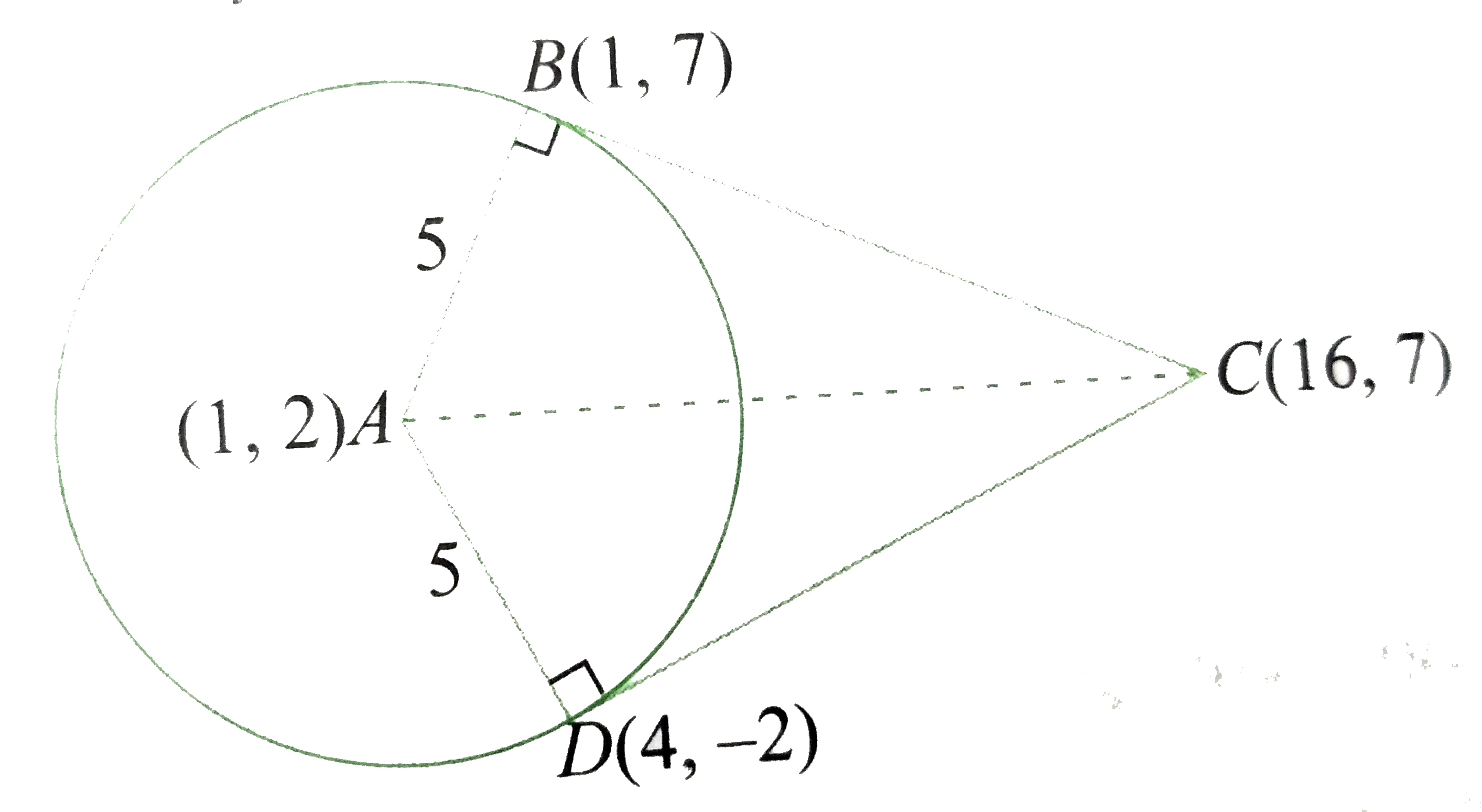
For point C, solving (1) and (2), we get `x=16` and `y=7` . Therefore, `C-= (16,7)`
Now, clearly ,
ar(quad. BCDA) `=2 xx ` ar (`Delta ABC)`
`=2 xx (1)/(2) xx AB xx BC`
`=AB xx BC`
where `AB=` Radius of circle `=5`
and `BC=15`
`:. ` ar (quad. ABCD) `= 5 xx 15=75 sq.` units