The locus fo the center of the circles such that the point (2, 3) is the midpoint of the chord 5x+2y=16 is 2x−5y+11=0 (b) 2x+5y−11=0 2x+5y+11=0 (d) none of theseSolution in Tamil
2x−5y+11=0
2x+5y−11=0
2x+5y+11=0
none of these
The correct Answer is:1
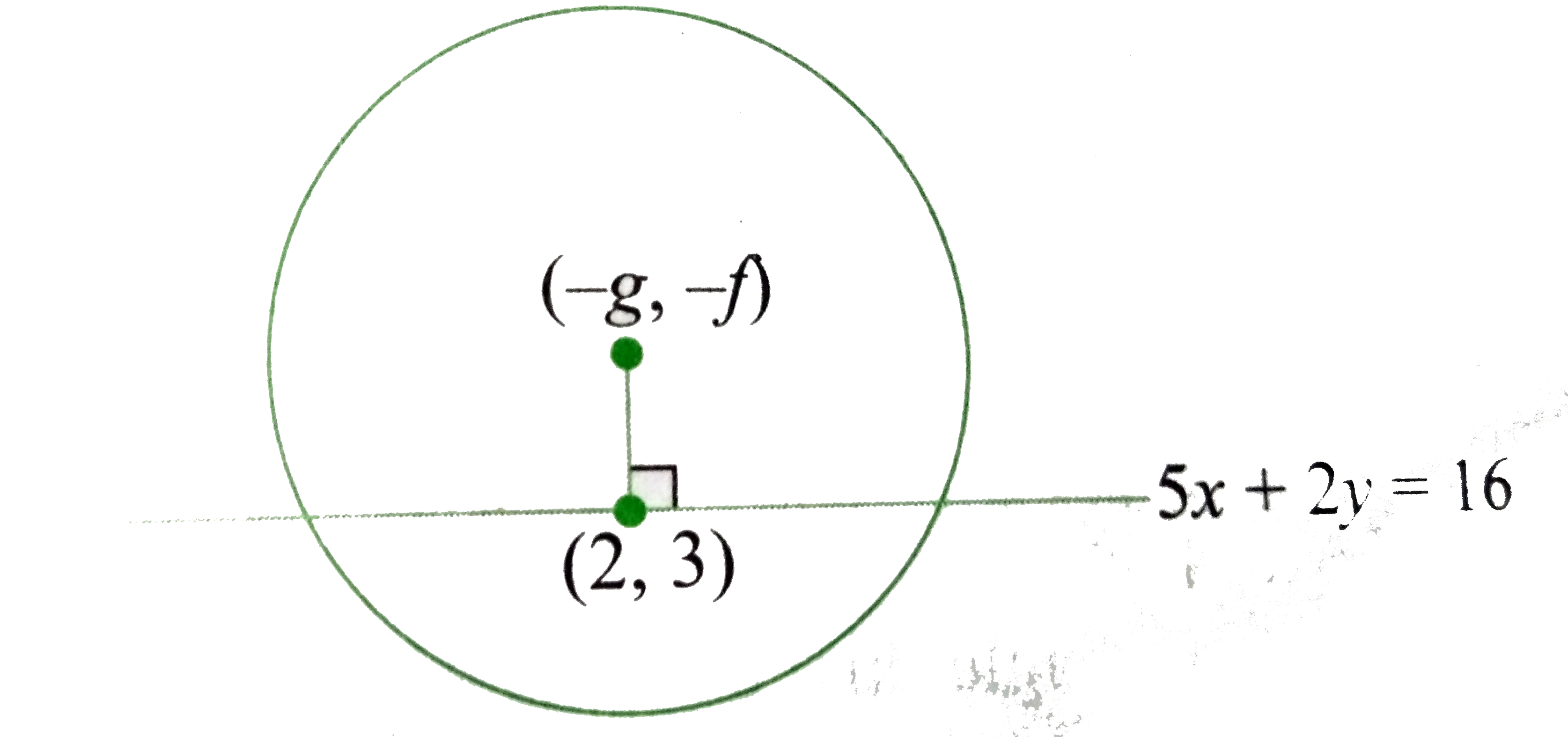
Slope of the given line =−52
∴(−52)(3+f2+g)=−1
or 15+5f=4+2g
Therefore, the locus is 2x−5+11=0
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
about to only mathematics
01:38View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
06:04View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
03:47View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is05:25View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionThe locus fo the center of the circles such that the point (2, 3) is the midpoint of the chord 5x+2y=16 is (a)2x−5y+11=0 (b) 2x+5y−11=0 (c)2x+5y+11=0 (d) none of these
01:26View Solutionसिद्ध कीजिए की सरल रेखाएं 2x+5y−1=0,3x−2y+8=0 तथा 7x+3y+11=0 संगामी है|
02:09View SolutionShow that the lines
2x+3y−8=0,x−5y+9=0and3x+4y−11=0 are concurrent.06:29View SolutionThe midpoint of the chord 4x+5y−13=0 of the ellipse 2x2+5y2=20 is
06:11View SolutionThe transformed equation of xy + 2x -5y - 11 = 0 when the origin is shifted to the point (2, 3) is,
03:55View SolutionWhen the axes are rotated through an angle 90° the equation 5x – 2y + 7 = 0 transforms to (A)2X−5Y+7=0(B)2X+5Y−7=0(C)2x−5Y–7=0(D)2X+5Y+7=0
04:47View SolutionThe transformed equation of xy + 2x -5y - 11 = 0 when the origin is shifted to the point (2, 3) is,
05:06View Solutionवृत्त 2x2+2y2−2x−5y+3=0 पर (1,1) से खींचें गए अभिलम्ब का समीकरण है
06:25View Solutionवृत्त x2+y2−6x+2y−54=0 की जीवा 2x - 5y + 18 = 0 के मध्य-बिंदु हैं
04:35View SolutionThe locus of the center of the circle such that the point (2,3) is the midpoint of the chord 5x+2y=16 is (a)2x−5y+11=0 (b) 2x+5y−11=0 (c)2x+5y+11=0 (d) none of these
04:53View SolutionThe combined equation of the asymptotes of the hyperbola 2x2+5xy+2y2+4x+5y=0 is (a) 2x2+5xy+2y2+4x+5y+2=0 (b) 2x2+5xy+2y2+4x+5y−2=0 (c)2x2+5xy+2y2=0 (d) none of these
02:16View Solution

