The area of the triangle formed by joining the origin to the point of intersection of the line x√5+2y=3√5 and the circle x2+y2=10 is 3 (b) 4 (c) 5 (d) 6
3
4
5
6
The correct Answer is:3
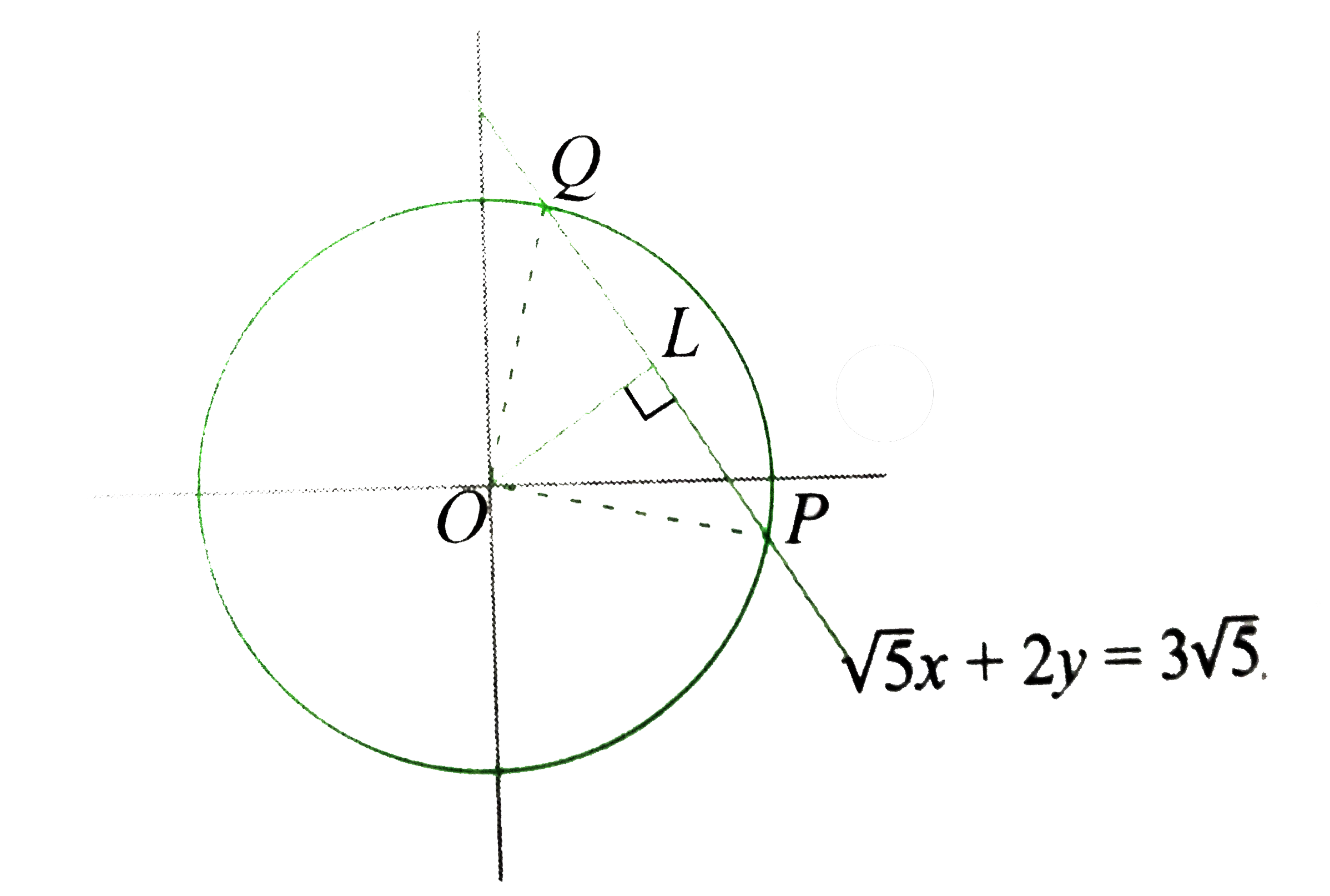
The length of perpendicular from the origin to the line x√5+2y=3√5 is
OL=3√5√(√5)2+22=3√5√9=√5
Radius of the given circle √10=OQ=OP
PQ=2QL=2√OQ2−OL2
2√10−5=2√5
Thus, area of ΔOPQ=12×PQ×OL
12×2√5×√5=5
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
The area of the triangle formed by joining the origin to the point of intersection of the line x√5+2y=3√5 and the circle x2+y2=10 is (a) 3 (b) 4 (c) 5 (d) 6
View SolutionThe area of the triangle formed by joining the origin to the point of intersection of the line x√5+2y=3√5 and the circle x2+y2=10 is
(a)3
(b) 4
(c) 5
(d) 6
View Solution
Knowledge Check
The area of the triangle formed by joining the origin to the point of intersection of the line x√5+2y=3√5 and the circle x2+y∘=10 is 3 (b) 4 (c) 5 (d) 6
A3B4C5D6The acute angle between the lines joining the origin to the points of intersection of the line √3x+y=2 and the circle x2+y2=4, is
Aπ2Bπ3Cπ4Dπ6The angle between the lines joining the origin to the points of intersection of the line √3x+y=2 and the curve y2−x2=4 is
Atan−1(2/√3)Bπ/6Ctan−1(√3/2)Dπ/2
The angle between the lines joining the origin to the points of intersection of the line √3x+y=2 and the curve y2−x2=4 is
View SolutionThe lines joining the origin to the points of intersection of the line 4x+3y=24 with the circle (x−3)2+(y−4)2=25 are
View SolutionThe lines joining the origin to the points of intersection of the line 4x+3y=24 with the circle (x−3)2+(y−4)2=25 are
View SolutionThe acute angle between the lines joining the orign to points of intersection of the line √3x+y=2 and the circle x2+y2=4 is
View SolutionThe lines joining the origin to the points of intersection of the line 4x−3y=10 with the circle x2+y2+3x−6y−20=0 are mutually perpendicular.
View Solution
