Any circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects these lines at points PandQ . Then the angle subtended by the arc PQ at its center is (a)1800 (b) 900 (c) 1200 depends on center and radiusSolution in Tamil
180∘
90∘
120∘
Depends on centre and radius
The correct Answer is:2
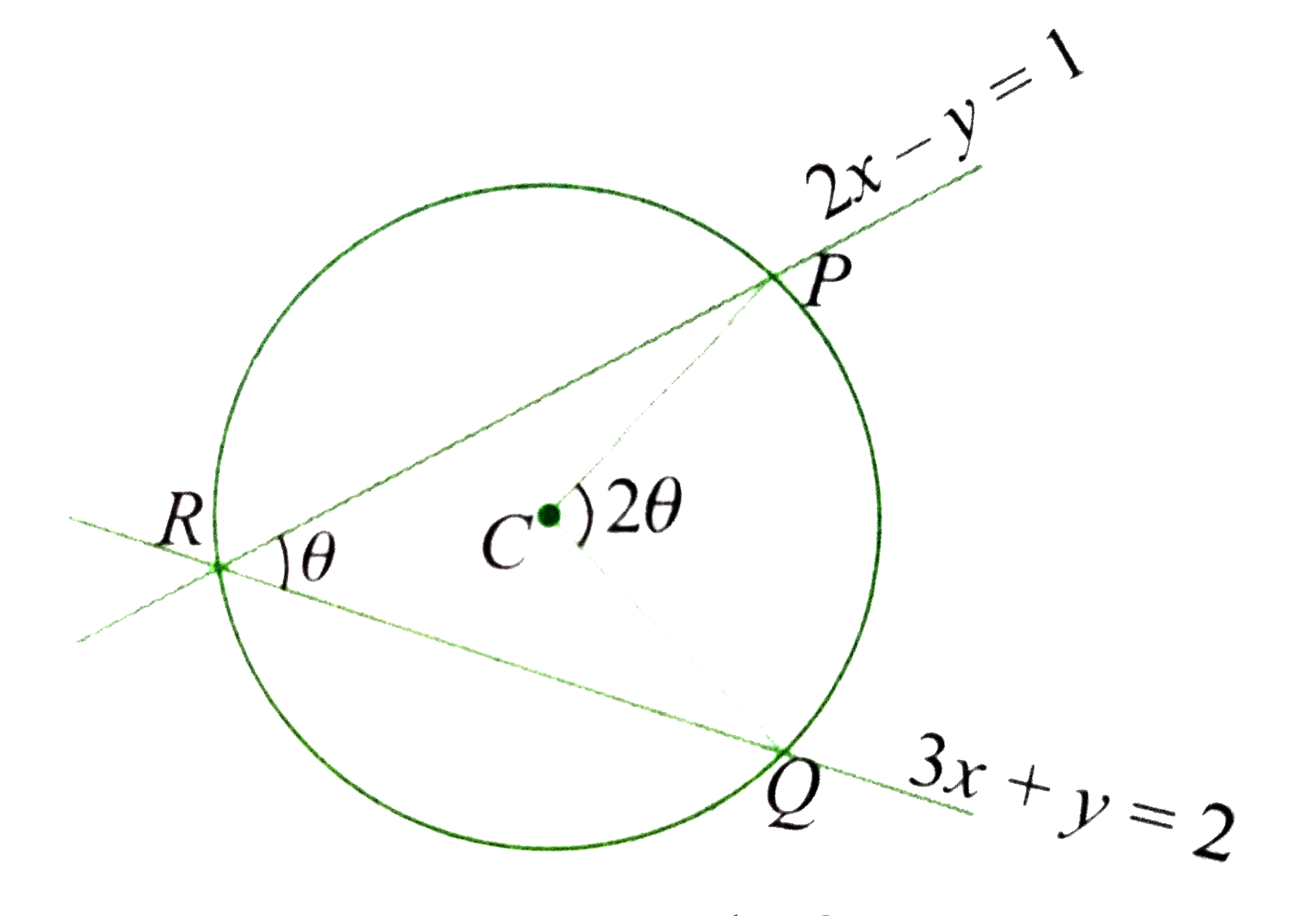
Slopes of gives lines are 2 and −3.
If angle between lines is θ , then
tanθ=∣∣∣2−(−3)1+(2)×(−3)∣∣∣=1
∴θ=∠PRQ=45∘
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionA straight line through the point (2,2) intersects the lines √3x+y=0 and √3x−y=0 at the point A and B, respectively. Then find the equation of the line AB so that triangle OAB is equilateral.
View SolutionAny circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects these lines at points PandQ . Then the angle subtended by the arc PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radius
View SolutionA circle passes through the points of intersection of the line x=0 and the circle x^(2)+y^(2)+2x=3. If this circle passes through (sqrt(3),0) then its centre is :
View Solutionरेखाओ x+3y=0 तथा 2x−7y=0 के प्रतिच्छेद बिंदु से जाने उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र रेखाओ x+y+1=0 तथा x−2y+4=0 का प्रतिच्छेद बिंदु है ।
View Solutionx+3y=0 तथा 2x−7y=0 के कटान बिन्दु से जाते हुए वृत्त का समीकरण निकाले जिसका केन्द्र रेखाओं x+y+1=0 तथा x−2y+4=0 का प्रतिच्छेद बिन्दु है।
View SolutionA straight line through the point (2, 2) intersects the lines √3x+y=0 and √3x−y=0 at the points A and B. The equation of the line AB so that ΔOAB is equilateral, is:
View SolutionA straight line through the point (2, 2) intersects the lines √3x+y=0 and √3x−y=0 at the points A and B. The equation to the line AB so that the triangle OAB is equilateral is
View SolutionA st. line through the point (2, 2) intersects the lines √3x+y=0and√3x−y=0 at the points A and B. The equation to the line AB so that the triangle OAB is equilateral is :
View Solutionமையம் (2, 3) உடையதும் 3x-2y-1=0 மற்றும் 4x+y-27=0 என்ற கோடுகள் வெட்டும் புள்ளி வழி செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
View SolutionAny circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects these lines at points PandQ . Then the angle subtended by the arc PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radius
View SolutionAny circle through the point of intersection of the lines x+√3y=1 and √3x−y=2 intersects there lines at points PandQ . Then the angle subtended by the are PQ at its center is 1800 (b) 900 (c) 1200 depends on center and radius
View Solution
