From an arbitrary point P on the circle x2+y2=9 , tangents are drawn to the circle x2+y2=1 , which meet x2+y2=9 at AandB . The locus of the point of intersection of tangents at AandB to the circle x2+y2=9 is x2+y2=(277)2 (b) x2−y2(277)2 y2−x2=(277)2 (d) none of theseSolution in Tamil
x2+y2=(27/7)2
x2−y2=(27/7)2
y2−x2=(27/7)2
none of these
The correct Answer is:1
Since ΔPOQ and ΔAOQ are congruent,
∠POQ=∠QOA=θ
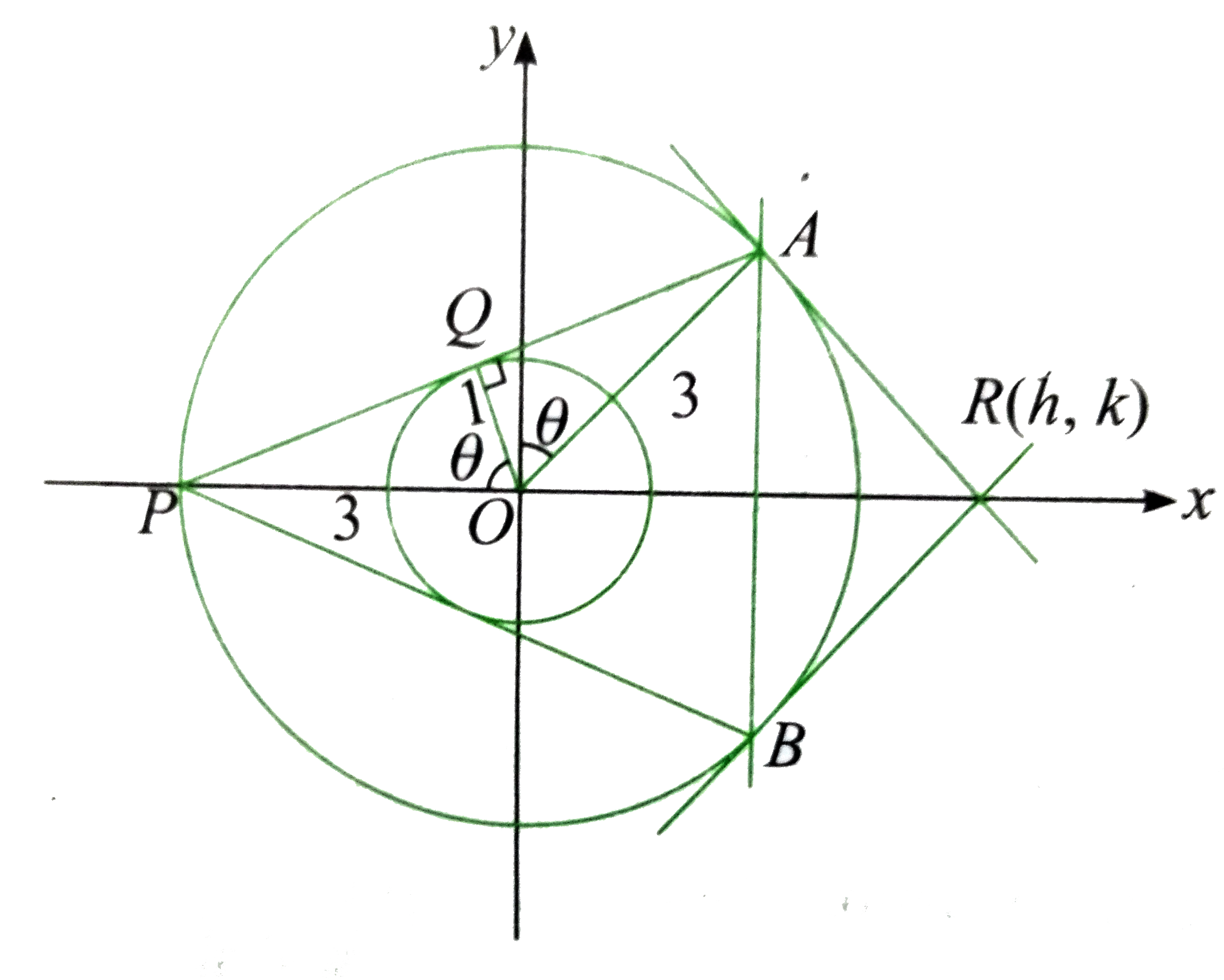
cosθ=12, since ∠POR=π
∴∠AOR=π−2θ
Now, in triangle AOR,∠AOR=π−2θ and AO=3 units
Therefore,
cos(π−2θ)=OAOR=3√h2+k2
or √h2+k2=277
or x2+y2=(277)2
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
about to only mathematics
03:18View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
04:52View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
05:23View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is07:05View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
04:13View SolutionThe tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
09:05View SolutionA tangent at a point on the circle x2+y2=a2 intersects a concentric circle C at two points PandQ . The tangents to the circle X at PandQ meet at a point on the circle x2+y2=b2. Then the equation of the circle is x2+y2=ab x2+y2=(a−b)2 x2+y2=(a+b)2 x2+y2=a2+b2
02:08View SolutionFrom an arbitrary point P on the circle x2+y2=9 , tangents are drawn to the circle x2+y2=1 , which meet x2+y2=9 at AandB . The locus of the point of intersection of tangents at AandB to the circle x2+y2=9 is x2+y2=(277)2 (b) x2−y2(277)2 y2−x2=(277)2 (d) none of these
04:41View SolutionTangents are drawn from any point on the hyperbola x29−y24=1 to the circle x2+y2=9 .If the locus of the mid-point of the chord of contact is a a(x2+y2)2=bx2−cy2 then the value of a2+b2+c27873
09:01View SolutionThe locus of the point of intersection of the perpendicular tangents to the circle x2+y2=a2,x2+y2=b is
06:30View SolutionTangents are drawn from points on the hyperbola x29−y24=1 to the circle x2+y2=9. Then show that the locus of the mid point of the chord of contact is (x2+y2)2=81(x29−y24)
01:55View SolutionTangents are drawn to the circle x2+y2=9 at the points where it is met by the circle x2+y2+3x+4y+2=0 . Find the point of intersection of these tangents.
03:18View SolutionA tangent at a point on the circle x2+y2=a2 intersects a concentric circle C at two points PandQ . The tangents to the circle X at PandQ meet at a point on the circle x2+y2=b2. Then the equation of the circle is x2+y2=ab x2+y2=(a−b)2 x2+y2=(a+b)2 x2+y2=a2+b2
06:43View SolutionFrom an arbitrary point P on the circle x2+y2=9 , tangents are drawn to the circle x2+y2=1 , which meet x2+y2=9 at A and B . The locus of the point of intersection of tangents at A and B to the circle x2+y2=9 is
(a) x2+y2=(277)2 (b) x2−y2(277)2 y2−x2=(277)2 (d) none of these02:06View SolutionIf the tangents to the parabola y2=4ax intersect the hyperbola x2a2−y2b2=1 at AandB , then find the locus of the point of intersection of the tangents at AandB.
04:26View SolutionThe circles x2+y2=9 and x2+y2−2y+27=0 touch each other. The equation of their common tangent is
02:26View Solution

