A circle C1 of radius b touches the circle x2+y2=a2 externally and has its centre on the positiveX-axis; another circle C2 of radius c touches the circle C1, externally and has its centre on the positive x-axis. Given a<b<c then three circles have a common tangent if a,b,c are in Solution in Tamil
AP
GP
HP
none of these
The correct Answer is:2
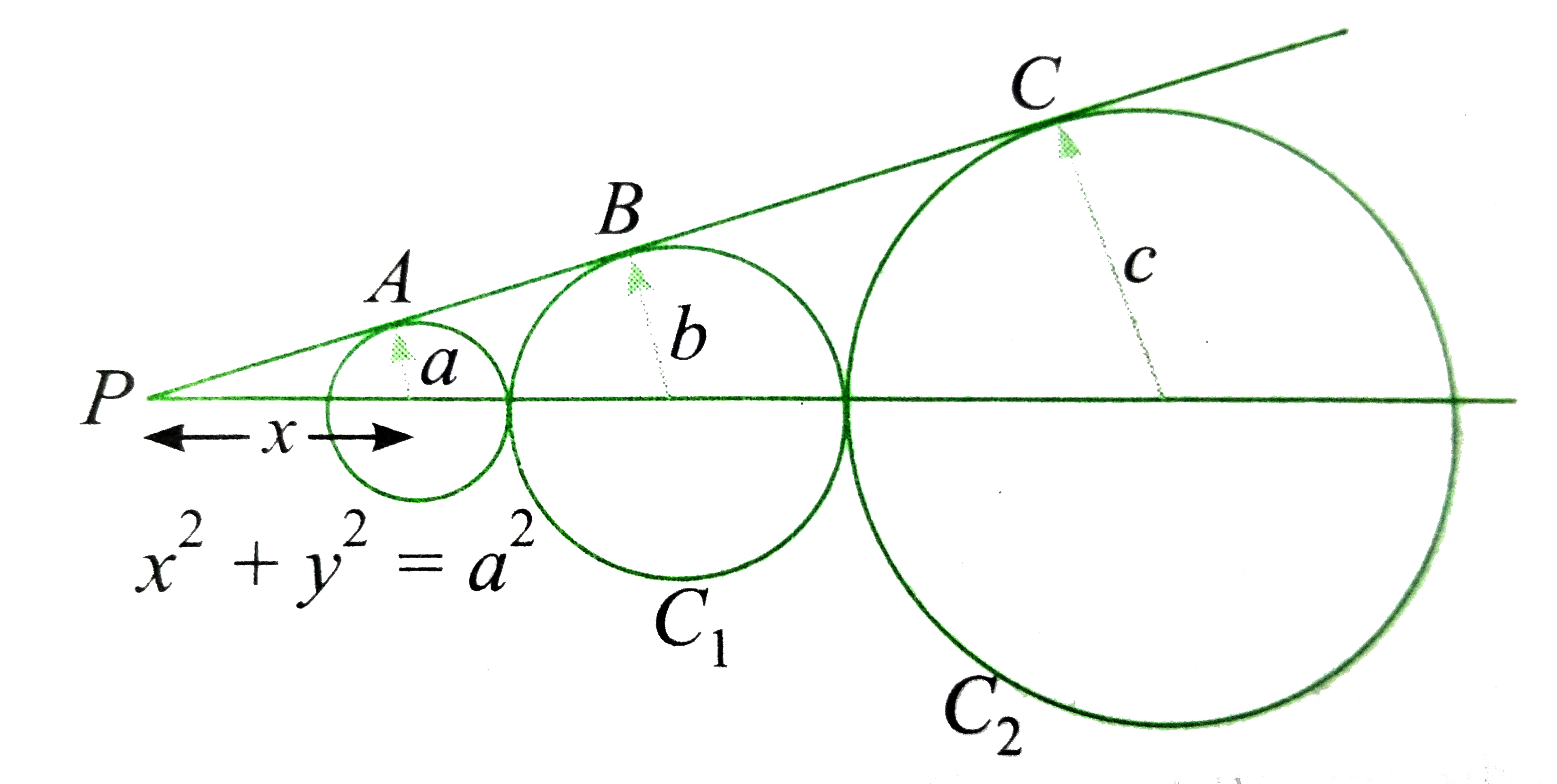
From the figure,
ax=bx+a+b=cxa+2b+c
∴ax+a2+ab=bx (Comparing first two )
or x=a2+abb−a
ax+a2+2ab+ac=cx (Comparing first and third )
∴a2+abb−a=a2+2ab+acc−a a2c−a3+abc−a2b=a2b+2ab2+abc−a3−2a2b−a2c
or ac=b2
Therefore, a,b, and c are in GP.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.65videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
about to only mathematics
05:01View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
02:39View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
04:51View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is04:41View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
04:59View SolutionThree circles,each of radius one,have centres at A,B and C. Circles A and B touch each other and circle C touches AB at its midpoint. The area inside circle C and outside circles A and B is
01:24View SolutionA circle c_1 of radius 2 units rolls on the other side of the circle c_2 : x^2+y^2+4x=0 ,touching its externally .The locus of the centre of this outer circle C_1, is the circle C_3 :
07:24View SolutionA circle C1 of radius b touches the circle x2+y2=a2 externally and has its centre on the positiveX-axis; another circle C2 of radius c touches the circle C1, externally and has its centre on the positive x-axis. Given a<b<c then three circles have a common tangent if a,b,c are in
04:24View SolutionC_1 and C_2 are fixed circles of radii r_1 and r_2 touches each other externally. Circle 'C' touches both Circles C_1 and C_2 extemelly. If r_1/r_2=3/2 then the eccentricity of the locus of centre of circles C is
04:44View Solution3 circles of radii a,b,c(a<b<c) touch each other externally and have x-axis as a common tangent then
03:12View SolutionIf a variable circle 'C' touches the x-axis and touches the circle x2+(y−1)2=1 externally, then the locus of centre of 'C' can be:
05:37View SolutionA circle C touches the x-axis and the circle x2+(y−1)2=1 externally, then locus of the centre of the circle C is given by
03:46View SolutionC1 is a circle of radius 1 and touching both the axis . C2 is another circle which touch both the axis and also circle C1 whose radius >1 then radius of C2 is
04:37View SolutionA circle C1 of radius b touches the circle x2+y2=a2 externally and has its centre on the positiveX-axis; another circle C2 of radius c touches the circle C1, externally and has its centre on the positive x-axis. Given a<b<c then three circles have a common tangent if a,b,c are in
06:31View SolutionA circle C1, of radius 2 touches both x-axis and y- axis. Another circle C1 whose radius is greater than 2 touches circle and both the axes. Then the radius of circle is (a) 6−4√2 (b) 6+4√2 (c) 3+2√3 (d) 6+√3
04:15View Solution3 circles of radii a,b,c(a<b<c) touch each other externally and have x-axis as a common tangent then
04:21View Solution

