An ellipse E,x2a2+y2b2=1, centred at point O has AB and CD as its major and minor axes, respectively. Let S1 be one of the foci of the ellipse, the radius of the incircle of triangle OCS1 be 1 unit, and OS1=6 units The perimeter of ΔOCS1 is Solution in Tamil
a) 20 units
b)10 units
c)15 units
d)25 units
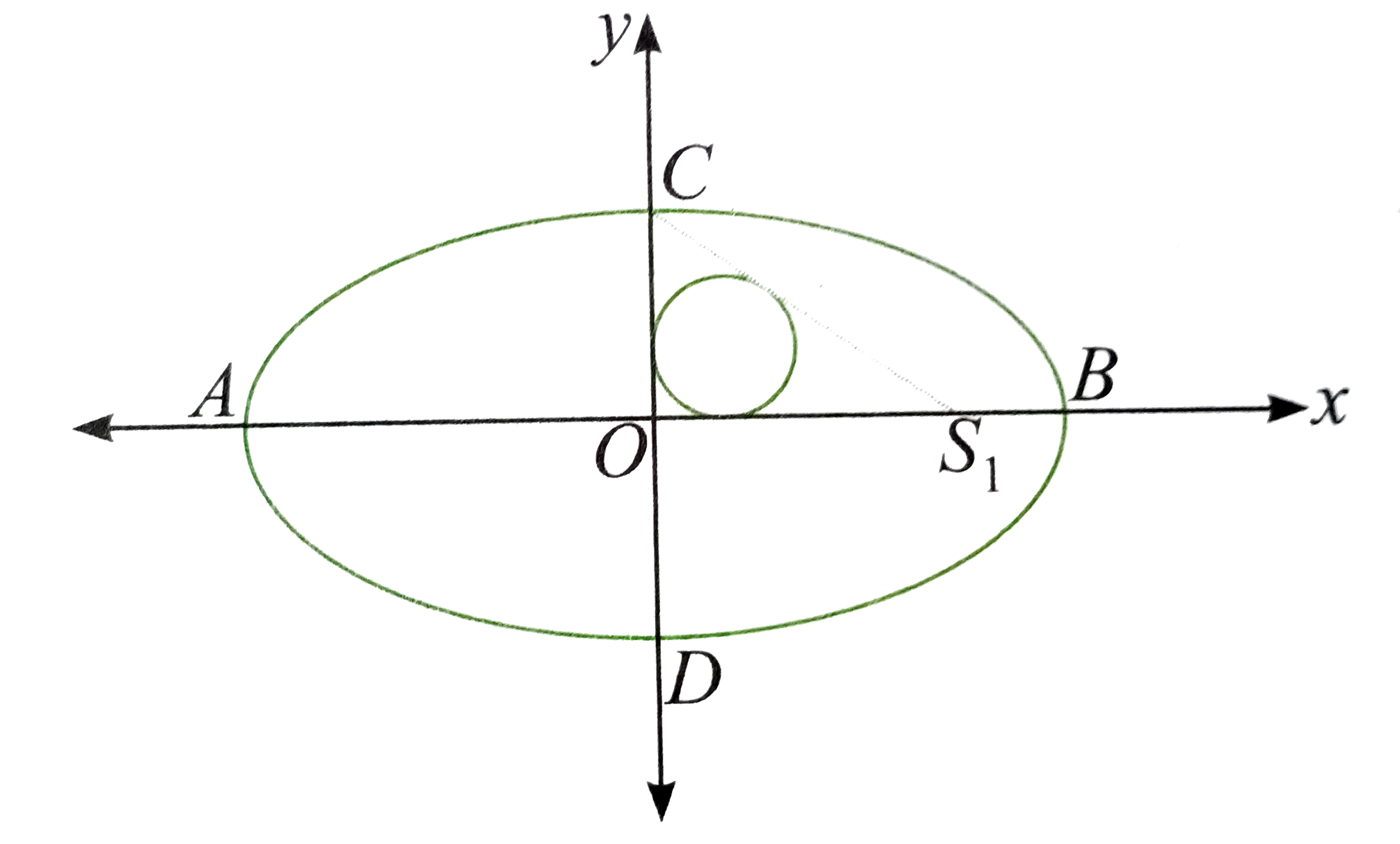
∴OS1=ae=6,OC=b
Also,CS1=a
∴Area of ΔOCS1=12=(OS1)×(OC)=3b
∴ Semi-perimeter of ΔOCS1=12=(OS1+OC+CS1)
=12(6+a+b) (1)
∴ In radius of ΔOCS1, (Usingr=ΔS)
=3b12(6+a+b)=1 (Usingr=ΔS)
or5b=6+a (2)
Also, b2=a2−a2e2=a2−36 (3)
From (2), we get
25(a2−36)=36+a2+12a
or2a2−a−78=0
a=132,−6
∴a=132andb=52
Area or ellipse =πab=65π4 sq. unit
Perimeter of ΔOCS1=6+a+b=6+132+52=15 units
The equation of director circle is
x2+y2=a2+b2
or x2+y2=972
Similar Questions
An ellipse has the points (1,−1)and(2,−1) as its foci and x+y=5 as one of its tangent then the value of a2+b2 where a,b are the lenghta of semi major and minor axes of ellipse respectively is :
05:53View Solutionएक दीर्घवृत्त (E)x2a2+y2b2=1, जिसका केन्द्र 'O' तथा AB तथा CD क्रमश: दीर्घ तथा लघु अक्षें है यदि S1 दीर्घवृत्त की एक नाभि, त्रिभुज OCS1 के अन्त:वृत्त की त्रिज्या 1 इकाई तथा OS1=6 इकाई हो, तो
दीर्घवृत्त (E) का क्षेत्रफल है04:14View Solutionएक दीर्घवृत्त (E)x2a2+y2b2=1, जिसका केन्द्र 'O' तथा AB तथा CD क्रमश: दीर्घ तथा लघु अक्षें है यदि S1 दीर्घवृत्त की एक नाभि, त्रिभुज OCS1 के अन्त:वृत्त की त्रिज्या 1 इकाई तथा OS1=6 इकाई हो, तो
ΔOCS का परिमाप है04:43View Solutionएक दीर्घवृत्त (E)x2a2+y2b2=1, जिसका केन्द्र 'O' तथा AB तथा CD क्रमश: दीर्घ तथा लघु अक्षें है यदि S1 दीर्घवृत्त की एक नाभि, त्रिभुज OCS1 के अन्त:वृत्त की त्रिज्या 1 इकाई तथा OS1=6 इकाई हो, तो
दीर्घवृत्त (E) का क्षेत्रफल है04:14View SolutionConsider an ellipse E:x2a2+y2b2=1, centered at point 'O' and having AB and CD as its major and minor axes respectively if S1be one of the focus of the ellipse, radius of the incircle of ΔOCS1 be 1 unit and OS1=6units. Q. The equation of the director circle of (E) is
09:44View SolutionS1 and S2 are the foci of an ellipse and B is the end of the minor axis. If the triangle S1S2B is an equilateral triangle, then eccentricity of the ellipse is
05:24View SolutionEquation of the ellipse is x2a2+y2b2=1 with foci S1andS2 The maximum area of the triangle PS1S2, where P is any point on the ellipse is
02:37View SolutionAn ellipse has the points (1,−1)and(2,−1) as its foci and x+y=5 as one of its tangent then the value of a2+b2 where a,b are the lenghta of semi major and minor axes of ellipse respectively is :
07:04View Solution

