[Tamil] A line OA of length r starts from its initial position OX and

If $cos θ - sin θ = \frac{1}{5}$ , where $0 < θ < \frac{π}{4}$ , then
ocr_image

If $f (θ) = \frac{1 - sin 2 θ + cos 2 θ}{2 cos 2 θ}$ , then value of $8 f (11^{0}) f (34^{0})$ is ____

If $cos β$ is the geometric mean between $sin α a n d cos α,$ where $0 < α, β < \frac{π}{2},$ then $cos 2 β$ is equal to $- 2 {sin}^{2} (\frac{π}{4} - α)$ (b) $- 2 {cos}^{2} (\frac{π}{4} + α)$ $- 2 s \in^{2} (\frac{π}{4} + α)$ (d) $2 {cos}^{2} (\frac{π}{4} - α)$

02:12

View Solution

The circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to

04:21

View Solution

If sec x + tan x =22/7 , find the value of tanx/2

06:56

View Solution

If sin alpha=(1)/(2) and cos theta=(1)/(3) then the values of alpha+theta( if theta,alpha are both acute angles) will lie in the interval

View Solution

sin(3 theta+alpha)+sin(3 theta-alpha)+sin(alpha-theta)-sin(alpha+theta)=cos alpha

05:52

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{1 - r cos α}{r sin α}$ is equal to

03:57

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{2 r sin α}{1 + 2 r cos α}$ is equal to

13:05

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
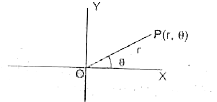
$\frac{2 r^{2} - 1}{r}$ is equal to

View Solution

Let $O P = r and ∠ X O P = θ$ then the position of P in polar coordinate system is represented by $(r, θ)$ OX and O are called the initial line and pole respectively.
If p be the length of perpendicular from origin to line and if $α$ is the angle which the perpendicular to the line makes with the initial line . The equation of line is given by r cos $(θ - α) = p$
ocr_image
Perpendicular distance from pole to the line $\frac{l}{r} = 4 cos θ + 2 sin θ$ is

13:05

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{2 r sin α}{1 + 2 r cos α}$ is equal to

View Solution

A line OA of length r starts from its initial position OX and traces an angle AOB = $α$ in the anitclockwise direction. It then traces back in the clockwise direction an angle BOC = $3 θ$ ( where $α > 3 θ$ ). L is the foot of the perpendicular from C on OA. Also, $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{2 r^{2} - 1}{r}$ is equal to

View Solution

A line OA length r starts from its initial position OX and traces an angle $A O B = α$ in the anticlockwise direction. It then traces back in the clockwise direction an angle $B O C = 3 θ$ ( where $α > 3 θ$ ) . L is the foot of the the perpendicular from C on OA. $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{1 - r cos α}{r sin α}$ is equal to

View Solution

A line OA length r starts from its initial position OX and traces an angle $A O B = α$ in the anticlockwise direction. It then traces back in the clockwise direction an angle $B O C = 3 θ$ ( where $α > 3 θ$ ) . L is the foot of the the perpendicular from C on OA. $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{2 r sin α}{1 + 2 r cos α}$ is equal to

View Solution

A line OA length r starts from its initial position OX and traces an angle $A O B = α$ in the anticlockwise direction. It then traces back in the clockwise direction an angle $B O C = 3 θ$ ( where $α > 3 θ$ ) . L is the foot of the the perpendicular from C on OA. $\frac{{sin}^{3} θ}{C L} = \frac{{cos}^{3} θ}{O L} = 1$
$\frac{1 - r cos α}{r sin α}$ is equal to

03:34

View Solution

The correct Answer is:D

Topper's Solved these Questions

Similar Questions

CENGAGE-TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS-Exercise (Comprehension)