A line x=k intersects the graph of y=log4x and y=log4(x+4). The distance between the points of intersection is 0.5, then the value of k is Solution in Tamil
1
2
3
4
The correct Answer is:D
We have log4(k+4)−log4x=0.5
⇒log4k+4k=0.5
⇒k+4k=2
⇒k=4
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - LOGARITHM AND ITS APPLICATIONS EXERCISE - Subjective Type9videos
LOGARITHM AND ITS APPLICATIONS
- BOOK - CENGAGECHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.210videos
LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS
- BOOK - CENGAGECHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE Previous Year5videos
LOGARITHM AND ITS PROPERTIES
Similar Questions
Find the value of x satisfying the equations log3(log2x)+log1/3(log1/2y)=1 and xy2=9
02:56View SolutionThe number of integral values of p for which (p+1)ˆi−3ˆj+pˆk,pˆi+(p+1)ˆj−3ˆk and −3ˆi+pˆj+(p+1)ˆk are linearly dependent vectors is q
02:54View SolutionShow that the equation esinx−e−sinx−4=0 has no real solution.
01:07View SolutionA line x=k intersects the graph of y=log_(4)x and y=log_(4)(x+4). The distance between the points of intersection is 0.5, then the value of k is
04:43View SolutionIf log_2 (log_3 (log_4 x))= 0, log_4 (log_3 (log_2 y))= 0 and log_3(log_4 (log_2z ))= 0, then the correct option is
02:55View SolutionIf log_2 x+log_4 y+log_4 z=2 then x^2yz=
04:39View SolutionIf log_2(log_3(log_4(x)))=0, log_3(log_4(log_2(y)))=0 and log_4(log_2(log_3(z)))=0 then the sum of x,y,z is
01:40View SolutionA line x=λ intersects the graph of y=log5x and y=log5(x+4).The distance between the point of intersection is 0.5. Given λ=a+√b,where a and b are integers , the value of (a+b) is
05:55View SolutionIF lines x−12=y+13=z−14andx−3=y−k2=z intersect then the value of k is
01:48View SolutionIf the graphs of x2=4(y+9) and x+ky=6 intersect on the x-axis , then k =
01:33View Solution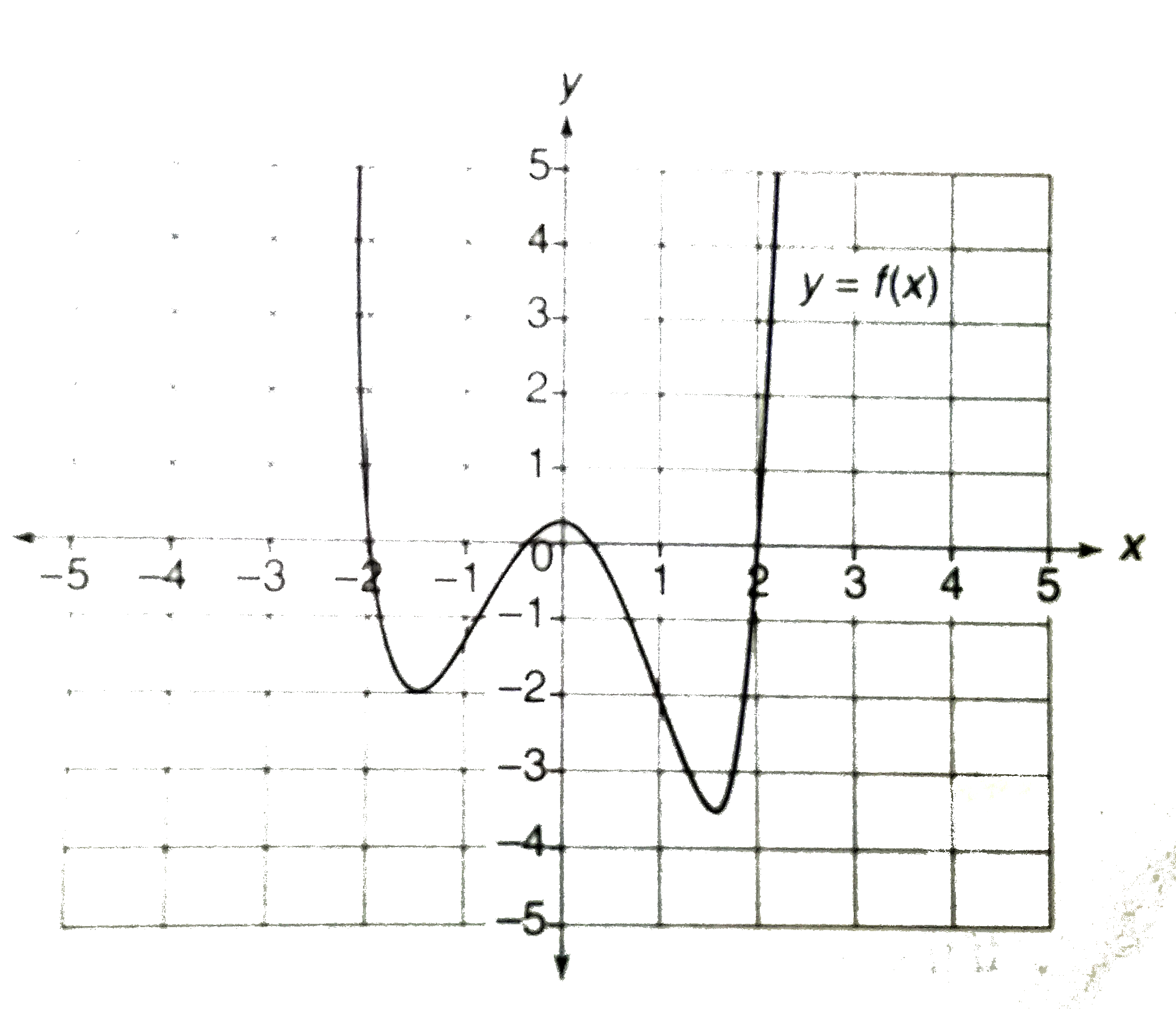
If g(x)=−2 intersects the graph of y=f(x)+k at one point, which of these choices could be the value of k?03:06View SolutionSolve : log48+log4(x+3)−log4(x−1)=2
04:37View SolutionSolve log4(8)+log4(x+3)−log4(x−1)=2
02:36View SolutionA line x=k intersects the graph of y=log4x and y=log4(x+4). The distance between the points of intersection is 0.5, then the value of k is
04:13View Solutionसरल रेखाओ xA+yB=k तथा xa−yb=1k जहाँ k एक अशून्य वास्तविक चर है, के प्रतिच्छेद बिन्दु का बिन्दुपथ है
01:43View SolutionFind the sum of 'n' terms of the series.
log2(xy)+log4(xy)2+log8(xy)3+log16(xy)4 +……..09:52View Solution

