Find all the value of $m$ for which the equation ${sin}^{2} x (m - 3) sin x + m = 0$ has real roots.

Text Solution

Verified by Experts

Put sin x = t , the equation is
$f (t) = t^{2} - (m - 3) t + m = 0$ (1)
Since sin x $\in$ [ -1, 1], the given equation will have real roots if (10 has at least root in [ - 1, 1].
Now (1) has real roots if ${(m - 3)}^{20 - 4 m \geq 0}$ . Thus ,
m $\in (- \infty, 1] \cup [9, \infty)$
If both roots in $[- 1, 1] t h e n f (1) = 4 > 0$ ,
$f (- 1) = 1 + m - 3 + m >$ ,
For m $>$ 1, Product of roots is greater then 1, which is not possible .
Therefore , exactly one root of (1) will lie in [-1, 1] .
Hence , $f (- 1) f (1) \leq 0$
$\Rightarrow (1 + m - 3 + m) (1 - m + 3 + m) \leq 0$
$\Rightarrow m \leq$ 1
Alternative Solution :
we have
$t^{2} \equiv (m - 3) t + M = 0$
or $t^{2} + 3 t = m (t - 1), w h e r e t \in$ [ -1, 1].
So, the graph of $y = t^{2} + 3 t$ must intersect the graph of $y = m (t - 1)$
at least once for t $\in [- 1, 1]$ .
Graph of $y = m (t - 1)$ is a line through (1, 0) and has veriable slope.
Graph of $y = t^{2} + 3 t$ is parabola passing though (0, 0) and (-3, 0) and concave upward.
Graph of both the relations are as as shown in the following figure.

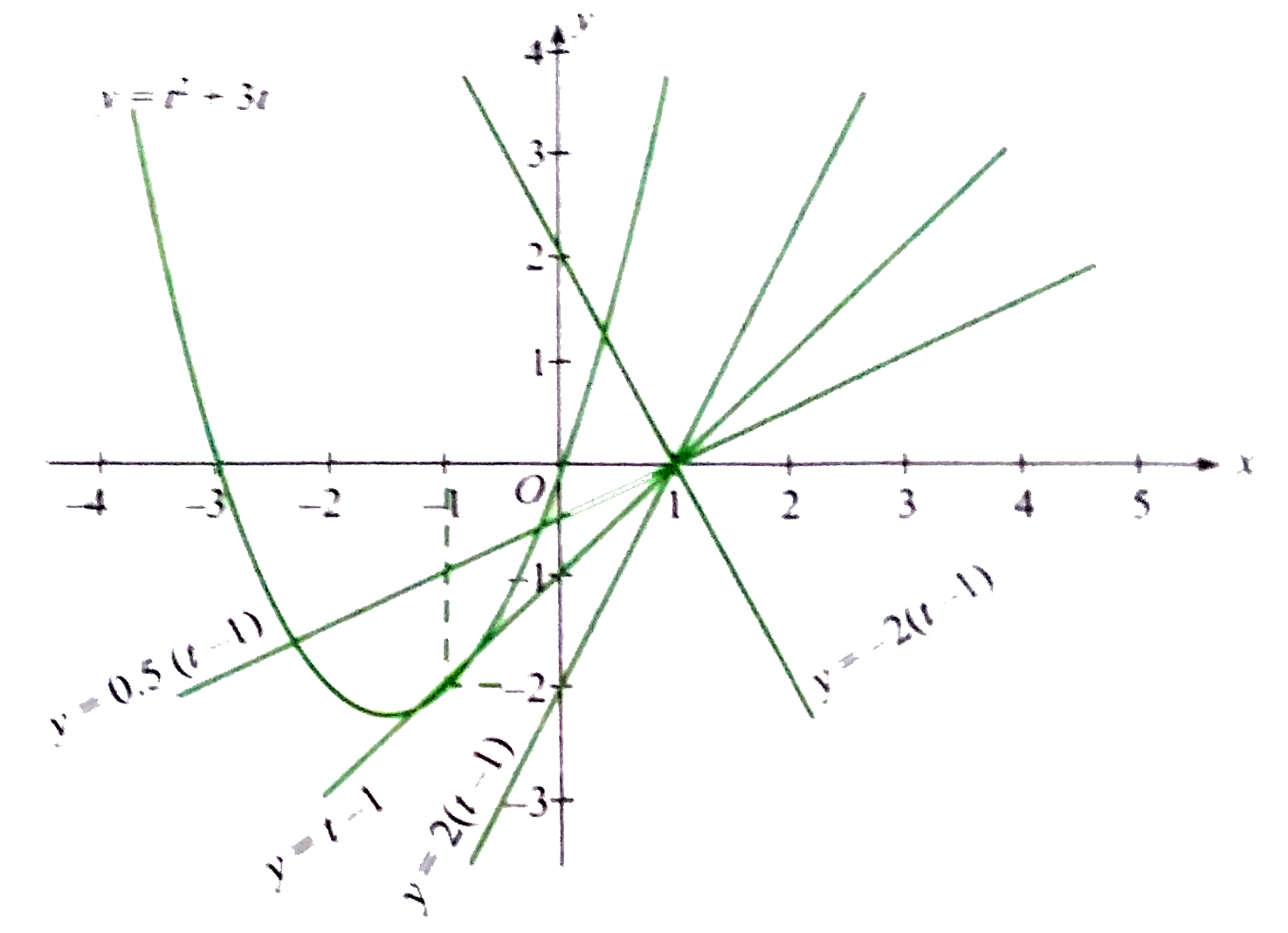
For parabola, $\frac{d y}{d t} = 2 t + 3 . S o {(\frac{d y}{d t})}_{(\begin{matrix} - 1 & - 2 \end{matrix})} = 1$ ,
Therefore, equation of tangent to parabola at (-1, -2) is y = t -1,
Which is line through (1, 0) .
Now , if slope of line than 1, then it intersect parabola for t $\in [- 1, 1]$ .
Thus, for solution of the equation $x^{2} + 3 t = m (t - 1)$ , we must have m $\leq$ 1.

Updated on:21/07/2023

The range of values of m for which the equation $(m - 5) x^{2} + 2 (m - 10) x + m + 10 = 0$ has real roots of the same sign, is given by
A $m > 10$
B $- 5 < m < 5$
C $m < - 10, 5 < m \leq 6$
Dnone of these
The number of integral values of m for which the equation $(1 + m^{2}) x^{2} - 2 (1 + 3 m) x + (1 + 8 m) = 0$ , has no real roots is
A1
B2
C3
Dinfinitely many