Consider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one real solutions for a∈.

A

(−∞,3)

B

[2,∞)

C

(3,∞)

D

[−2,∞)

Text Solution
Verified by Experts

The correct Answer is:2

Given that 9x−a3x−a+3≤0
Let t=3x. Then,
t2−at−a+3≤0
or t3+3≤a(t+1) (1)
where t∈R+,∀x∈R
Let f1(t)=t2+3 and
f2(t)=a(t+1).
In this case both graphs should meet at least once is t∈(0,∞). For a= 2 both the curves touch , hence the required range is a∈[2,∞)
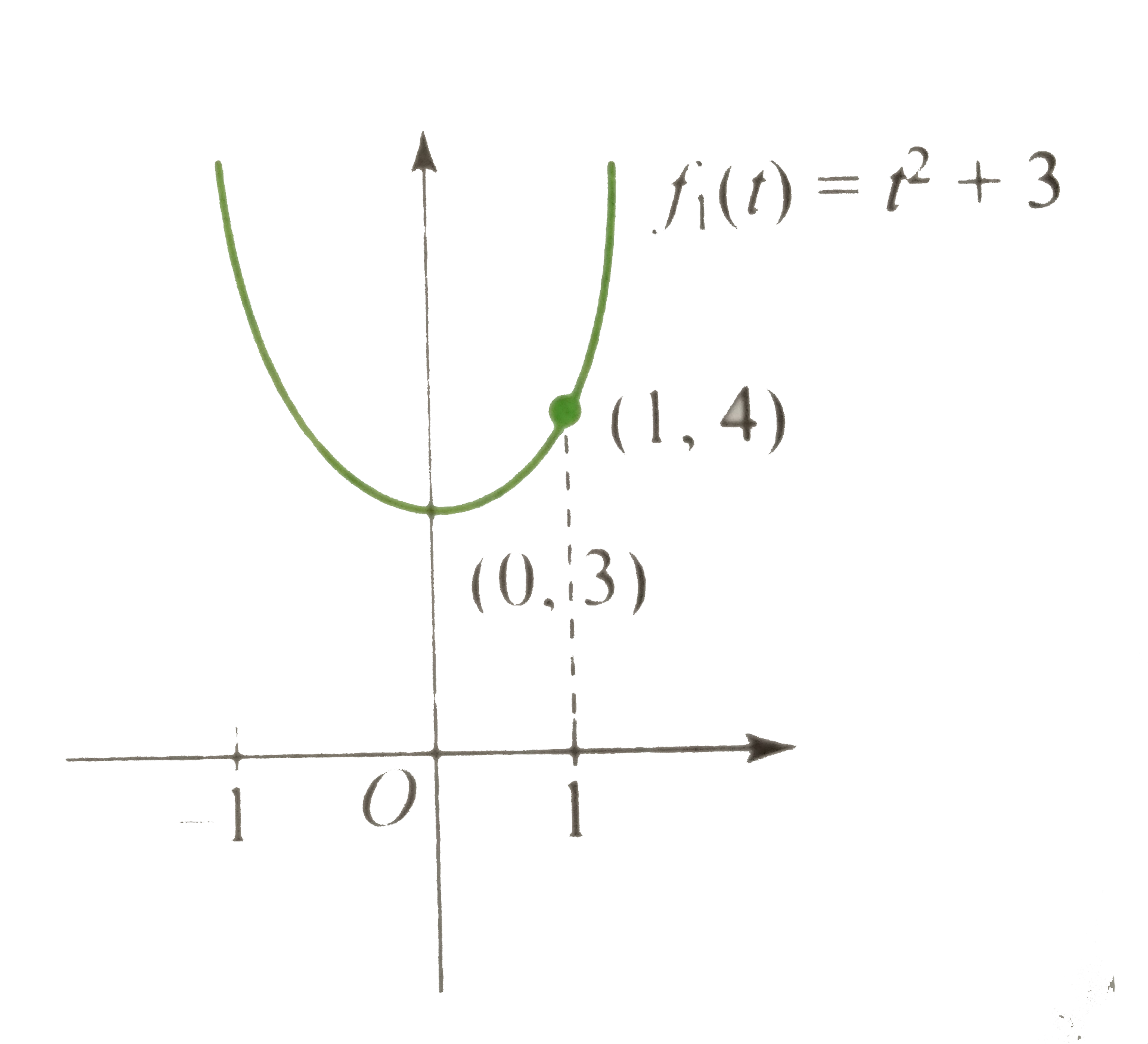
ocr_image

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSQUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Consider the inequation 9x−a3x−a+3≤0, where a is real parameter.
    The given inequality has at least one negative soluiton for a∈

    A(−∞,2)
    B(3,∞)
    C(−2,∞)
    D(2,3)

  • Consider the inequation x2+x+a−9<0
    The values of the real parameter a so that the given inequations has at least one negative solution.

    A(−∞,9)
    B(374,∞)
    C(−∞,374)
    Dnone of these

  • Consider the inequation x2+x+a−9<0
    The values of the real parameter a so that the given inequaiton has at least one positive solution:

    A(−∞,37/4)
    B(−∞,∞)
    C(3,∞)
    D(−∞,9)