Consider the quadratic equation ax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of c is
Option 1: 4
Option 2 : 6
Optiom 3: 7
Option 4: 5
Solution in Tamil
4
6
7
5
The correct Answer is:2
az2−bx+c=0
Let f(x)=ax2−bx+cbe
the correspoding quadratic expression and α,β be the roots of f(x)=0.
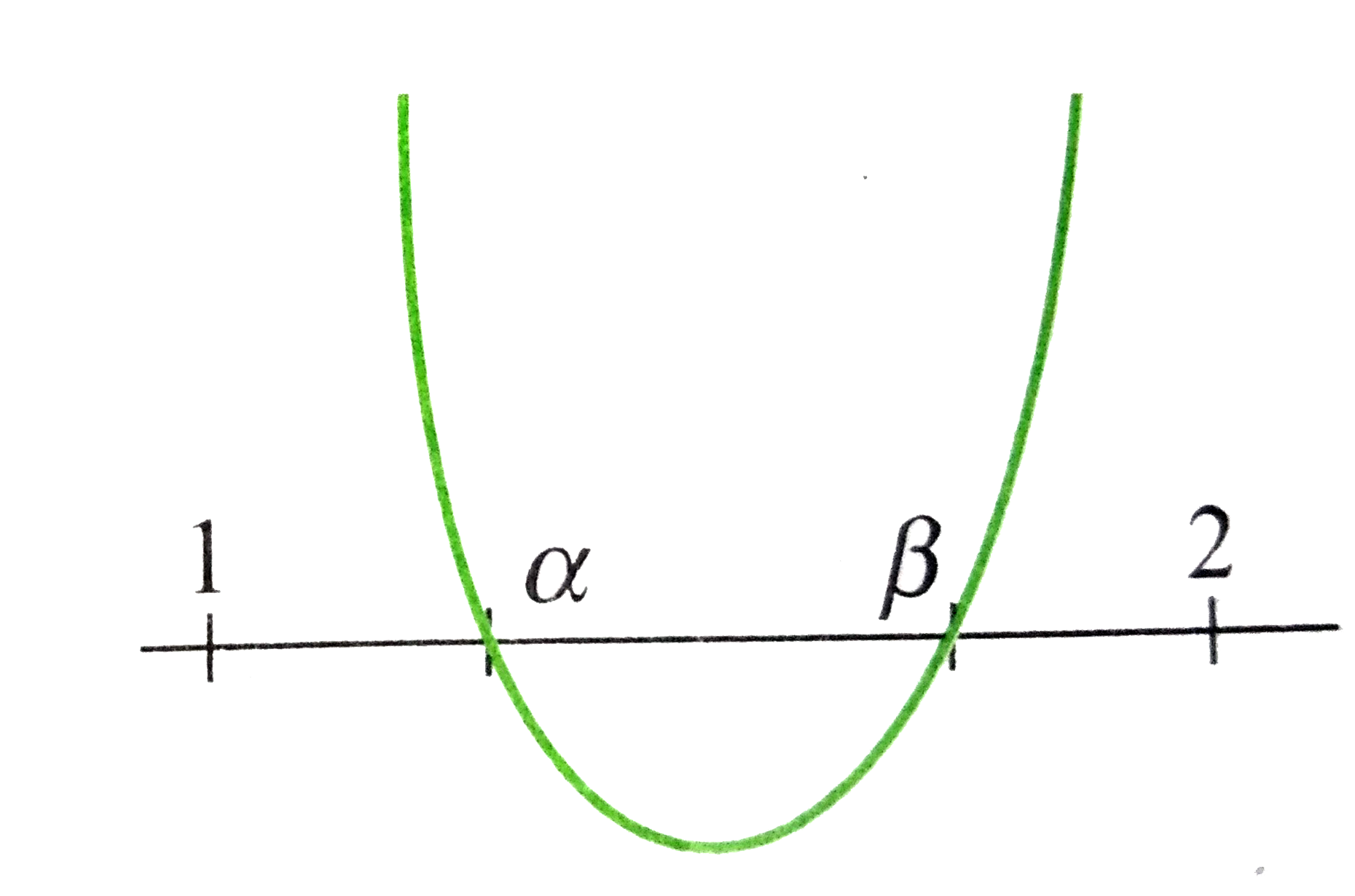
Then, f(x)=a(x−α)(x−β)
Now, af(1)>0,af(2)>0,1<b2a<2,b2−4ac>0
⇒a(1−α)(1−β)>0,a(2−α)(2−β)>0,2a<b<4a,b2−4ax>0
⇒a2(1−α)(1−β)(2−α)(2−β)>0
⇒a2(1−α)(1−β)(2−α)(2−β)>0
As f(x) and f(2) both are integers and f(1)>0, and f(2)>0, so
f(1)f(2)>0
⇒f(1)f(2)>1
⇒1≥a2(α−1)(2−α)(β−1)(2−β) (1)
Now, (α−1)+(2−α)2>((α−1)(2−α))1/2
⇒(α−1)(2−α)≤14
Similarly,
(β−1)(2−β)≤14
⇒(α−1)(2−α)(β−1)(2−β)<116
As α≠β, so α2>1 (Using (1))
⇒a>5
⇒b2>20candb>10⇒b≥11
Also, b2>100⇒c>5⇒c≥6
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Matrix)6videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Numerical)43videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Multiple)38videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year4videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank12videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Match the following for the equation x2+a|x|+1=0 where, a is a parameter.
 10:00View Solution
10:00View SolutionIf x=2+223+213, then the value of x3−6x2+6x is:
06:59View Solutionif c≠0 and the equation p2x=ax+c+bx−c has two equal roots, then p can be
View Solutionabout to only mathematics
View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
View SolutionIf ax2−bx+c=0 have two distinct roots lying in the interval (0,1);a,b,∈N, then the least value of a , is
06:01View SolutionThe quadratic equation ax2+bx+c=0 has real roots if:
08:28View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of a is04:30View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of b is08:02View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of c is04:32View SolutionA quadratic equation ax2+bx+c=0has two distinct real roots, if….
02:32View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of b is04:06View SolutionIf ax2−bx+c=0 have two distinct roots lying in the interval (0,1);a,b,∈N, then the least value of a , is
05:18View SolutionIfax2−bx+c=0 has two distinct roots lying in the interval (0,1),a,b,c∈N. Then
05:52View SolutionThe quadratic equation ax2+bx+c=0 has real roots if:
06:55View Solution

