Prove that apb&q>(ap+bpp+q)p+q.
Text Solution
Consider p quantities each point equal to a and q quantities each equal to b. we know that
A.M.>G.M.
∴(a+a+..... to p terms)+(b+b+....to q terms)p+q
>[(ca×a.... to p factors )(b×b.....to q factors )]1p+q
⇒ap+bqp+q>(apbq)1p+q
⇒(ap+bqp+q)p+q>(apbq) lt
|
Topper's Solved these Questions
- INEQUALITIES INVOLVING MEANS BOOK - CENGAGECHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Exercise 6.4
4 Videos
- INEQUALITIES INVOLVING MEANS BOOK - CENGAGECHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Exercise (Single)
20 Videos
- INEQUALITIES INVOLVING MEANS BOOK - CENGAGECHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Exercise 6.2
6 Videos
- INEQUALITIES AND MODULUSBOOK - CENGAGECHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer
21 Videos
- INTEGRALSBOOK - CENGAGECHAPTER - INTEGRALSEXERCISE - Solved Examples And Exercises
222 Videos
Similar Questions
Prove that apbq<(ap+bqp+q)p+q.
View SolutionProve that apbq<(ap+bqp+q)p+q.
View SolutionProve that q∧~p≡~(q→p)
View SolutionProve that q∧~p≡~(q→p)
View SolutionThe sums of first p, q, r terms of an A.P. are a, b, c respectively. Prove that
ap(q−r)+bq(r−p)+cr(p−q)=0
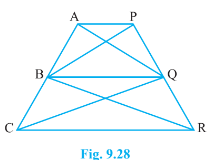
View SolutionIn Fig.9.28, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).
View SolutionIn Figure PQ∣∣CD and PR∣∣CB.ProveAQQD=ARRB.
View SolutionShow that: |xpqpxqqqx|=(x−p)(x2+px−2q2).
View SolutionThe pth term of an A.P. is a and qth term is b Prove that the sum of its (p+q) terms is p+q2{a+b+a−bp−q}.
View SolutionSum of the first p, q and r terms of an A.P are a, b and c, respectively.Prove that ap(q−r)+bq(r−p)+cr(p−q)=0
View Solution
