The largest area of the trapezium inscribed in a semi-circle or radius R, if the lower base is on the diameter, is 3√34R2 (b) √32R2 3√38R2 (d) R2
(3√34R2)
(√32R2)
(3√38R2)
R2
The correct Answer is:1

AD=ABcosθ=2Rcosθ
AE=ADcosθ=2Rcos2θ
EF=AB−2AE=2R−4Rcos2θ
DE=Adsinθ=2Rsinθcosθ
Thus area of trapezilum
S=12(AB+CD)×DE
=12(2R+2R−4Rcos2θ)×2Rsinθcosθ
=4R2sin3θcosθ
dsdθ=12R2sin2θcos2θ−4R2sin4θ
=4R2sin2θ(3cos2θ−sin2θ)
For maximum are dsdθ=0ortan2θ=3
or tanθ=√3(θisacute)orSmax=3√34R2
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Multiple)
40 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Comprehension)
42 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise 6.7
5 Videos
- METHODS OF DIFFERETIATIONBOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank
13 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
The largest area of the trapezium inscribed in a semi-circle or radius R, if the lower base is on the diameter, is (a) 3√34R2 (b) √32R2 3√38R2 (d) R2
View SolutionThe largest area of the trapezium inscribed in a semi-circle or radius R, if the lower base is on the diameter, is 3√34R2 (b) √32R2 3√38R2 (d) R2
View Solution
Knowledge Check
Three circles of radius 1 cm are circumscribed by a circle of radius r, as shown in the figure. Find the value of r?
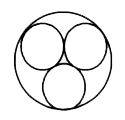
(a)√3+1
(b)2+√3√3
(c)√3+2√2
(d)2+√3A√3+1B2+√3√3C√3+2√2D2+√3
A cone is circumscribed about a sphere of radius R. The volume of the cone is minimum if its height is: (A) 3R (B) 4R (C) 5R (D) 2√2R
View SolutionProve that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 6√3r.
View SolutionProve that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 6√3r
View SolutionThe volume of the largest possible cube that can be inscribed in a hollow spherical ball of radius r cm is 2√3r2 (b) 43r2 (c) 83√3r3 (d) 13√3r3
View SolutionThree equal circles each of radius r touch one another. The radius of the circle touching all the three given circles internally is (2+√3)r (b) (2+√3)√3r (2−√3)√3r (d) (2−√3)r
View SolutionProve that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 6√3r.
View SolutionProve that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 6√3r.
View Solution
