Two runner A and B start at the origin and run along positive x axis ,with B running three times as fast as A. An obsever, standeing one unit above the origin , keeps A and B in view.Then the maximum angle theta of sight between the observer's view of A and B is Solution in Tamil
The correct Answer is:2
and
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Multiple)40videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Comprehension)42videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise 6.75videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank13videos
METHODS OF DIFFERETIATION
- BOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Let f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x2+3x,−1≤x<0−sinx,0≤x<π/2−1−cosx,π2≤x≤π . Draw the graph of the function and find the following
(a) Range of the function
(b) Point of inflection
(c) Point of local minima04:35View Solutionf(x)=sin−1x+x2−3x+x33,x∈[0,1]
04:05View SolutionA metal box with a square base and vertical sides is to contain 1024 cm3 of water, the material for the top and bottom costs Rs 5 per cm2 and the material for the sides costs Rs 2.50 per cm2. Find the least cost of the box.
06:54View SolutionLet f:(−5,5)→R be a differentiable function with f(4) = 1, f′(4)=1,f(0)=−1 and f^(')(0) = 1,Ifg(x) = f(2f^(2)(x)+2))^(2),then - g^(')(0) equals
View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?03:20View SolutionThree particles A,B and C start from the origin at the same time, A with a velocity a along x -axis, B with a velocity b along y -axis and C with velocity c in XY plane along the line x=y .The magnitude of c so that the three always remain collinear is:
03:58View SolutionVelocity time graphs of particles A and B moving along x-axis are shown here. Both A and B start from origin:
 04:42View Solution
04:42View SolutionTwo particles A and B start from the origin along x-axis. Velocity time graph of both particles are shown in the figure. During the given time interval, the maximum separation between the particles is
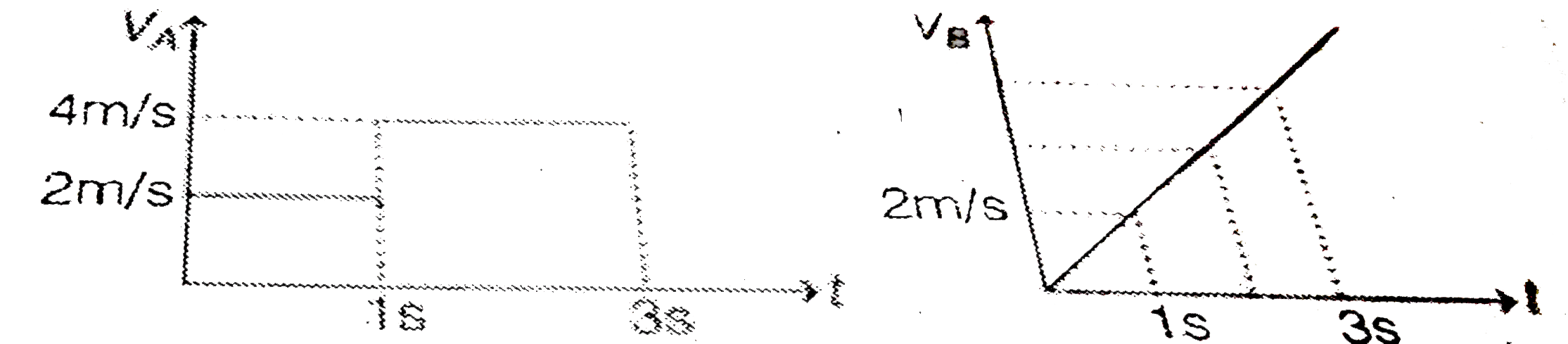 06:39View Solution
06:39View SolutionTwo runner A and B start at the origin and run along positive x axis ,with B running three times as fast as A. An obsever, standeing one unit above the origin , keeps A and B in view.Then the maximum angle theta of sight between the observer's view of A and B is
View Solutionमूल बिंदु से ऊपर y -अक्ष को 2 इकाई कि दूरी पर प्रतिच्छेद करने वाली और x -की धन दिशा के साथ 30∘ का कोण बनाने वाली रेखा का समीकरण ज्ञात कीजिए।
10:37View Solutionदो लड़के भूमि के दो छोरो A और B पर खड़े है , जहाँ AB = a है | B पर खड़ा लड़का v1वेग से AB के लंबवत दिशा में दौड़ना प्रारंभकरता है |उसी समय A पर खड़ा लड़का v वेग से दौड़ना प्रारंभ करता है और समय में दूसरे लड़के को पकड़ लेता है |t का मान होगा -
View Solutionदो कण A और Bके समय - विस्थापन वक्र सरल रेखाएँ हैं जो समय अक्ष के साथ क्रमशः 30∘ व 60∘ कोण बनाते हैं | इनके वेगों vA:vB में अनुपात होगा
View SolutionLet A and B are two points on X -axis and y -axis respectively and circle passes , through A,B and O (origin).Tangent at origin is at a distance of 3 unit and 5 unit from point A and B respectively, then radius of circle is
05:19View SolutionThree particles A, B & C start from the origin at the same time, A with a velocity 'a' along x-axis, B with a velocity 'b' along y-axis and C with velocity 'c' in XY plane along the line x = y. The magnitude of 'c' so that the three always remain collinear is:
06:15View SolutionTwo runner A and B start at the origin and run along positive x axis ,with B running three times as fast as A. An obsever, standeing one unit above the origin , keeps A and B in view.Then the maximum angle theta of sight between the observer's view of A and B is
03:58View Solution

