Discuss the applicability of Rolles theorem for the following
functions on the indicated intervals:
f(x)=|x|∈[−1,1]
f(x)=3+(x−2)2/3
in [1,3]
f(x)=tanx∈[0,π]
f(x)=log{x2+abx(a+b)}
in [a,b], where 0 less than a less than bSolution in Tamil
Step by step video & image solution for Discuss the applicability of Rolles theorem for the following functions on the indicated intervals: f(x)=|x|in[-1,1] f(x)=3+(x-2)^(2//3) in [1,3] f(x)=tanx in [0,pi] f(x)=log{(x^2+a b)/(x(a+b))} in [a,b], where 0 less than a less than b by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - ILLUSTRATION
2 Videos
- APPLICATION OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - SOLVED EXAMPLES
1 Videos
- APPLICATION OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - JEE Previous Year
9 Videos
- 3D COORDINATION SYSTEM BOOK - CENGAGECHAPTER - 3D COORDINATION SYSTEM EXERCISE - DPP 3.1
11 Videos
- APPLICATION OF INTEGRALSBOOK - CENGAGECHAPTER - APPLICATION OF INTEGRALSEXERCISE - Solved Examples And Exercises
17 Videos
Similar Questions
Find Distance between the points for which lines that pass through the point (1,1) and are tangent to the curve represent parametrically as x=2t−t2 and y=t+t2
View SolutionIf f"(x) exists for all points in [a,b] and
f(c)−f(a)c−a=f(b)−f(c)b−c,wherea<c<b, then show that there exists a number 'k' such that f"(k)=0.
View SolutionThe shortest distance between line y-x=1 and curve x=y2 is
View SolutionGiven two points A and B. If area of triangle ABC is constant then locus of point C in space is
View SolutionIf the area by y=x2+2x−3 and the line y=kx+1 is the least, find k and also the least area.
View SolutionVerify Rolle theorem for the function f(x)=log{x2+abx(a+b)}on[a,b], where 0<a<b.
View SolutionDiscuss the applicability of Rolles theorem for the following functions on the indicated intervals: f(x)=|x|∈[−1,1] f(x)=3+(x−2)2/3 in [1,3] f(x)=tanξn[0,π] f(x)=log{x2+abx(a+b)} in [a,b],where≺a<b
View SolutionDiscuss the applicability of Rolles theorem for the function f(x)=3+(x−2)2/3 on [1, 3]
View SolutionVerify Rolles theorem for the function f(x)=log{x2+abx(a+b)} on [a, b] , where 0<a<b .
View SolutionDiscuss the applicability of Rolles theorem for the function f(x)=3+(x−2)2/3 on [1, 3]
View Solutionअन्तराल [a, b] में फलन f(x)=log{x2+abx(a+b)},0<a<b के लिए रोले प्रमेय का सत्यापन कीजिए।
View SolutionThe function f(x) is defined in (−3,2). Then, the domain of f(|[x]|) is ([x] denotes the greatest integer less than or equal to x)
(A) [0, 3)
(B) [-2, 3)
(C) [-2, 2]
(D) [0, 2]
View SolutionBX3 में B−X दुरी उस दुरी की तुलना कम होती है जिसे सैद्धान्तिक रूप से अपेक्षित किया जाता है क्योकि
(X=F,C1,Br,I)
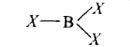
View SolutionDiscuss the applicability of Rolles theorem for the following functions on the indicated intervals: f(x)=|x|∈[−1,1] f(x)=3+(x−2)2/3 in [1,3] f(x)=tanξn[0,π] f(x)=log{x2+abx(a+b)} in [a,b],where≺a<b
View SolutionDiscuss the applicability of Rolles theorem for the following functions on the indicated intervals: f(x)=|x|∈[−1,1] f(x)=3+(x−2)2/3 in [1,3] f(x)=tanξn[0,π] f(x)=log{x2+abx(a+b)} in [a,b],where≺a<b
View SolutionVerify Rolle theorem for the function f(x)=log{x2+abx(a+b)}on[a,b], where 0<a<b.
View Solution
