Let a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα⟨−1andβ⟩1 , then show that 1+ca+∣∣∣ba∣∣∣<0Solution in Tamil
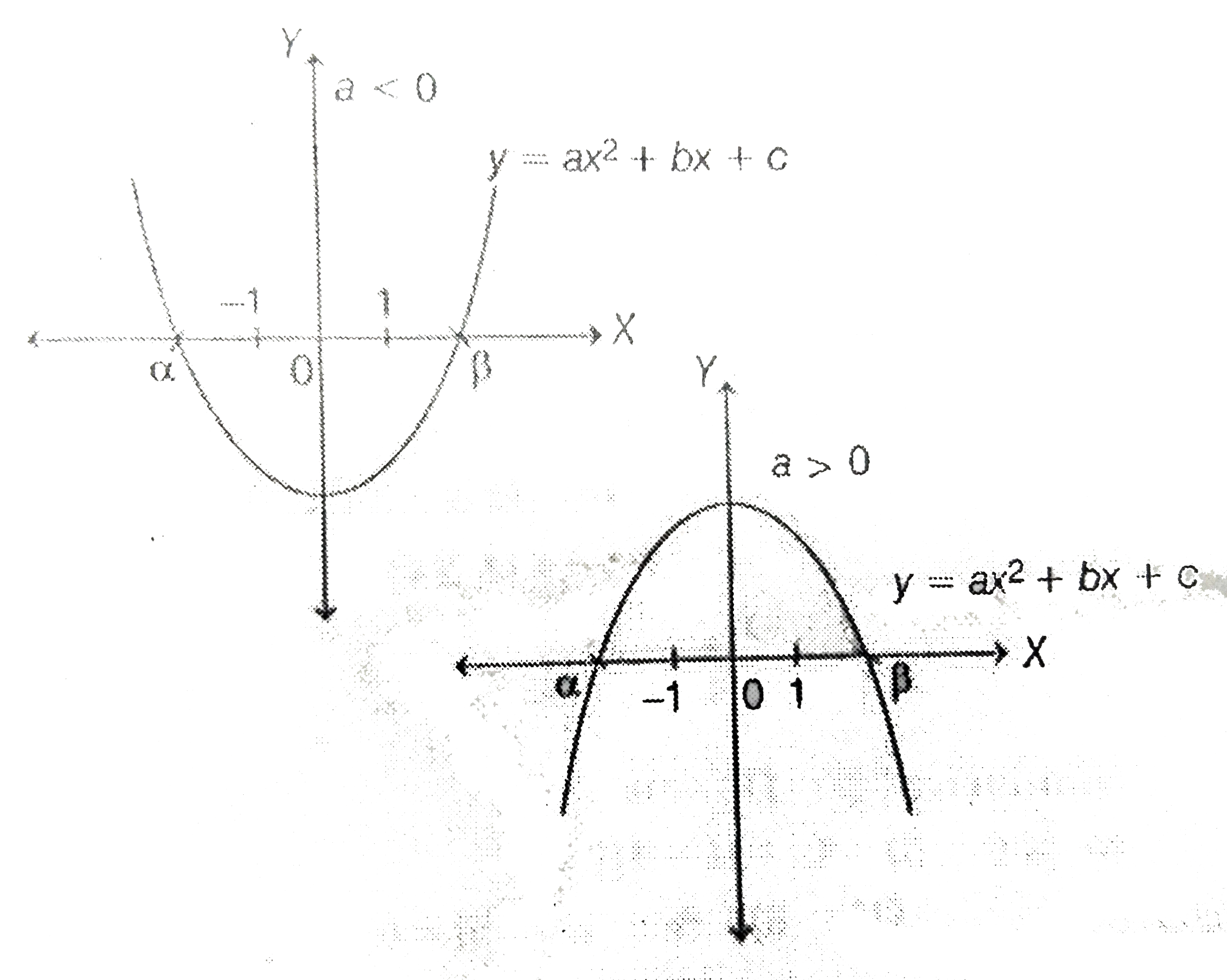
From figure it is clear that, if a>0, then f(−1)<0andf(1)<0andifa>0,f(−1)>0andf(1)>0. In both cases, af(−1)<0andaf(1)<0.
⇒a(a−b+c)<0anda(a+b+c)<0
on dividing by a2, we get
1−ba+ca<0and1+ba+ca<0
On combining both, we get
1±ba+ca<0
⇒a+∣∣∣ba∣∣∣+ca<0
Similar Questions
Let a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα⟨−1andβ⟩−1 , then show that 1+ca+∣∣∣ba∣∣∣<0
01:49View SolutionIf αandβ are roots of the quadratic equation ax2+bx+c=0 and a+b+c>0,a−b+c>0&c<0,then[α]+[β] is equal to (where [.] denotes the greatest integer function) (a)10 (b) −3 (c) −1 (d) 0
02:57View SolutionIf α is a real root of the quadratic equation ax2+bx+c=0andβ ils a real root of −ax2+bx+c=0, then show that there is a root γ of equation (a/2)x2+bx+c=0 whilch lies between α&β
03:58View SolutionConsider two complex numbers αandβ as α=[(a+bi)/(a−bi)]2+[(a−bi)/(a+bi)]2, where a ,b , in R and β=(z−1)/(z+1),where|z|=1, then find the correct statement: (a)both αandβ are purely real (b)both αandβ are purely imaginary (c)α is purely real andβ is purely imaginary (d)β is purely real and α is purely imaginary
06:56View SolutionIf ax2+(b−c)x+a−b−c=0 has unequal real roots for all c∈R,then
03:55View SolutionIf αandβ are the roots of ax2+bx+c=0andSn=αn+βn, then aSn+1+bSn+cSn−1=0
03:08View SolutionIf αandβ(α<β) are the roots of the equation x2+bx−c=0,whereb<0<c, then 0<α<β b. α<0<β<|α| c. α<β<0 d. α<0<|α|<β
04:37View Solution

