For reaction the rate constant and for the reactio the rate constant . If and cal /mol, cal/mol then the temperature at which is (Given :R=2 cal/K-mol)
a) 1200 K
b)
c)
d) Solution in Punjabi
1200 K
The correct Answer is:D
Step by step video & image solution for For reaction ArarrB, the rate constant k_(1)=A_(1) e^(-Ea_(1//(RT))) and for the reactio XrarrY, the rate constant k_(2)=A_(2) e^(-Ea_(2//(RT))) . If A_(1)=10^(8),A_(2)=10^(10) and E_(a_(1))=600 cal /mol, E_(a_(2))=1800 cal/mol then the temperature at which k_(1)=k_(2) is (Given :R=2 cal/K-mol) a) 1200 K b) 1200xx4.606 K c) (1200)/(4.606)K d) (600)/(4.606)K by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 2 (Q.33 To Q.35)
2 Videos
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 3 - Passage
1 Videos
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 2
1 Videos
- SURFACE CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level -2
1 Videos
Similar Questions
In a sample of wood, the reading of a counter is 32 dpm and in a fresh sample of tree it is 122dpm . Due to error counter gives the reading 2 dpm in absence of .14C . Half life of .14C is 5770 years .
The approximate age (in years) of wood sample is :
View SolutionTwo consecutive irreversible first order reactions can be represented by
Ak1−−→Bk2−−→C
The rate equation for A is readily interated to obtain
[A]t=[A]0.e−k1t , and [B]t=k1[A]0k2−k1[e−k1(t)−e−k2(t)]
When k1=1s−1 and k2=500s−1 , select most appropriate graph
a)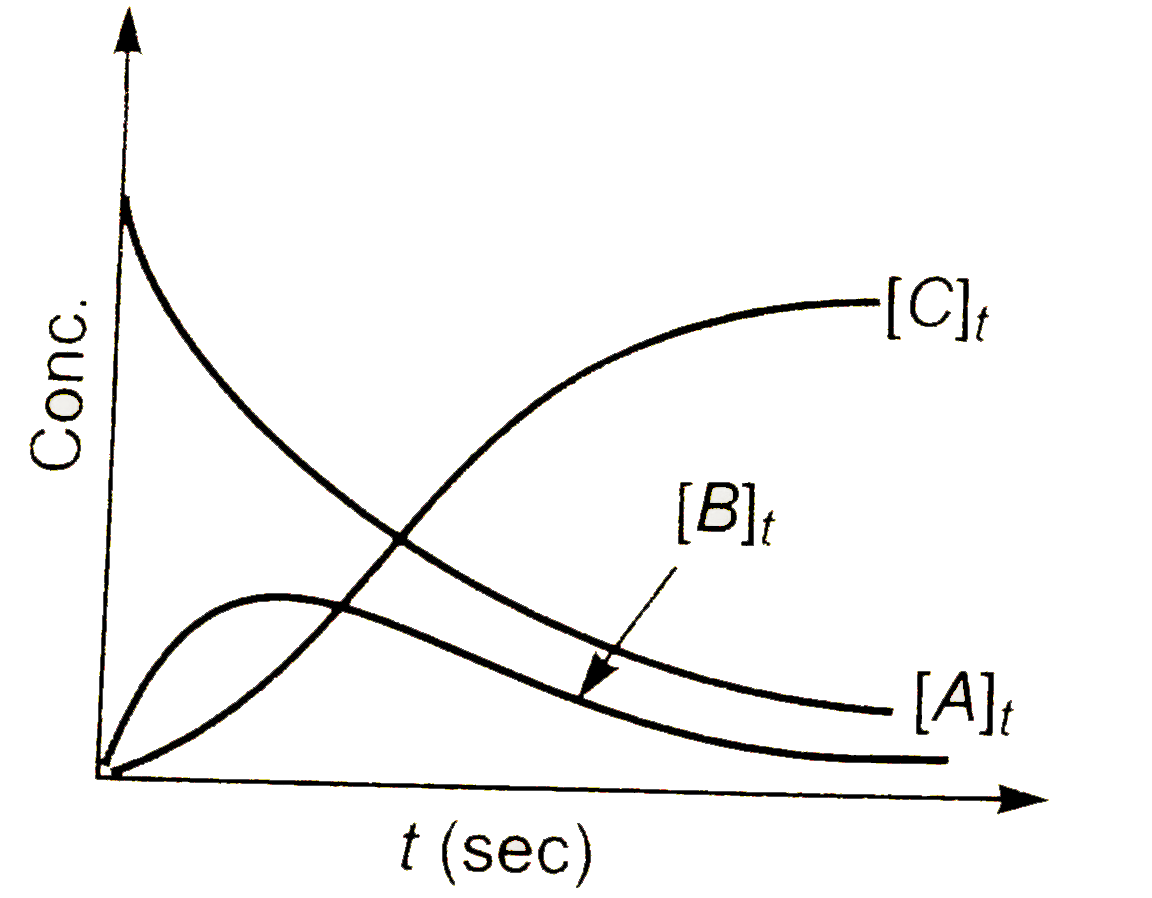 b)
b) 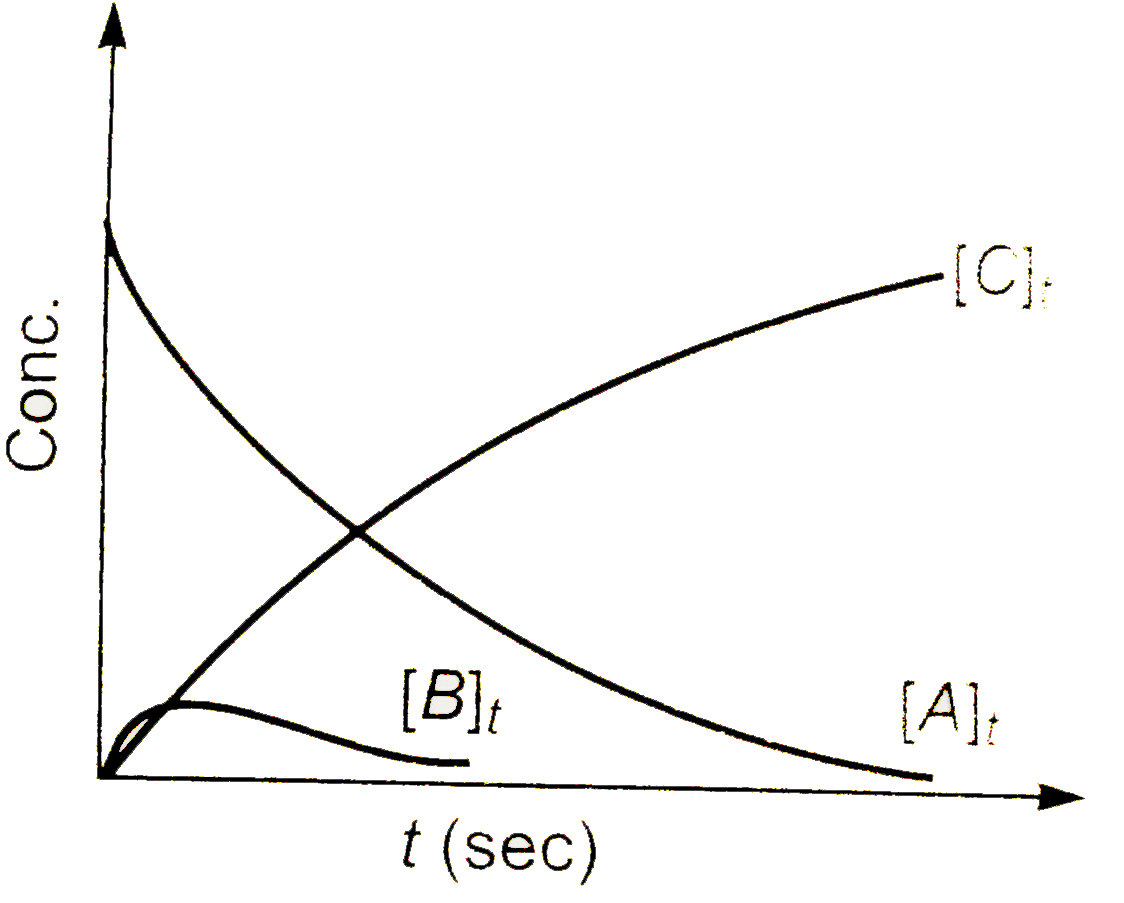
c)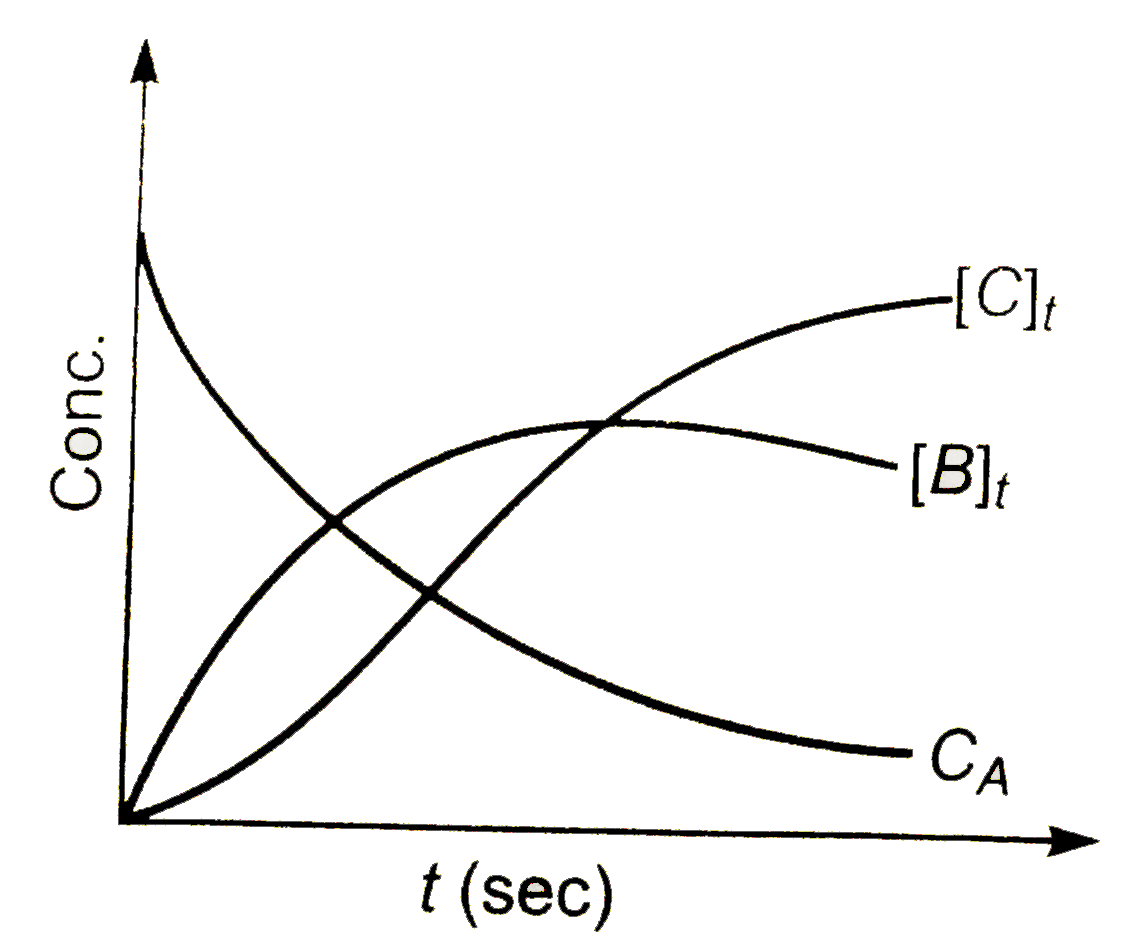 d)
d) 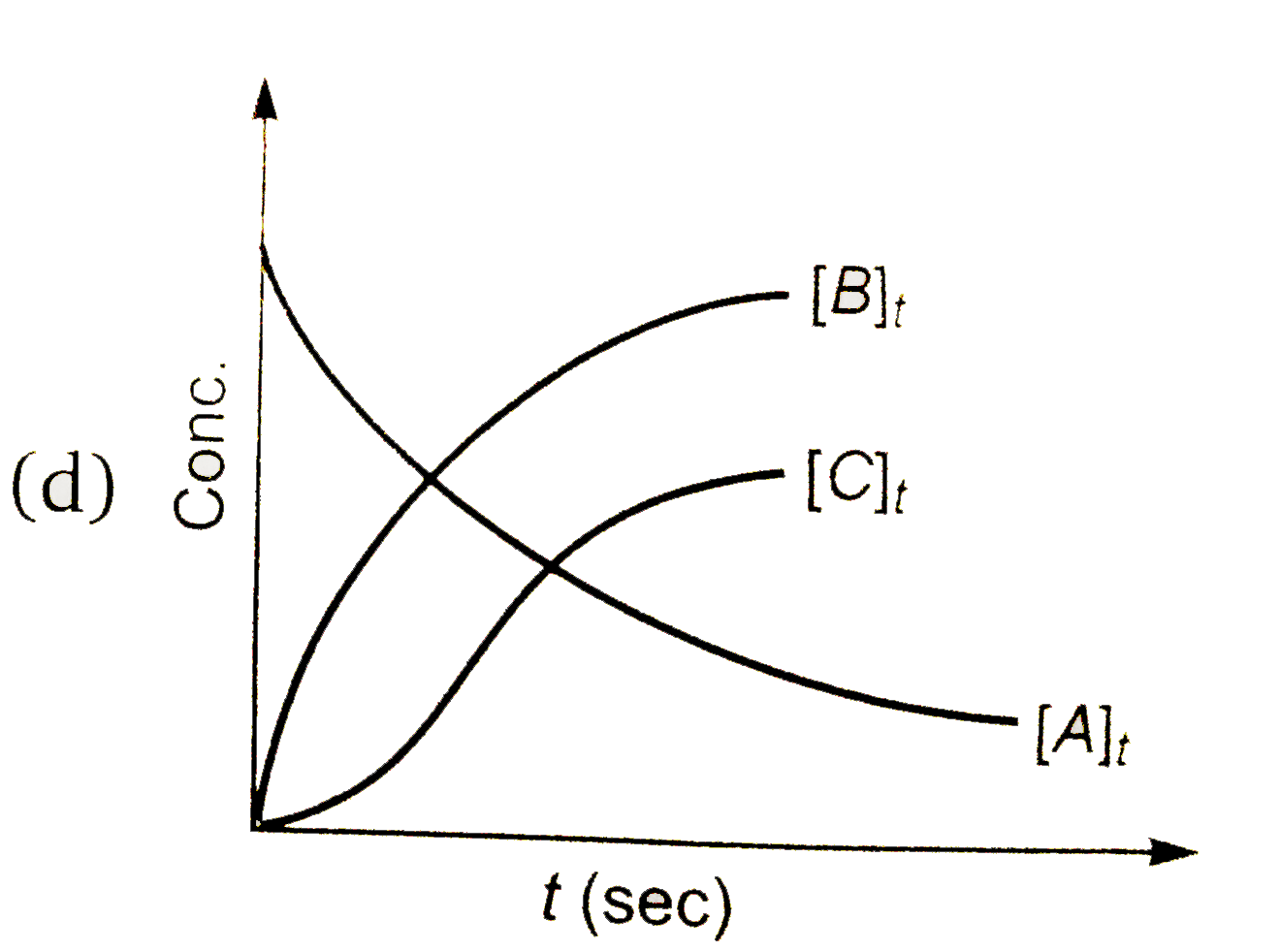
View SolutionThe forward rate constant for the elementary reversible gaseous reaction
C2H6<⇒2CH3is1.57×10−3s−1at100K
What is the rate constant for the backward reaction at this temperature if 10−4 moles of CH3 and 10 moles of C2H6 are present in a 10 litre vessel at equilibrium .
a) 1.57×109Lmole−1s−1
b) 1.57×1010Lmole−1s−1
c) 1.57×1011Lmole−1s−1
d) 1.57×107Lmole−1s−1
View Solutionfor the graph below, select correct order of temperture ?
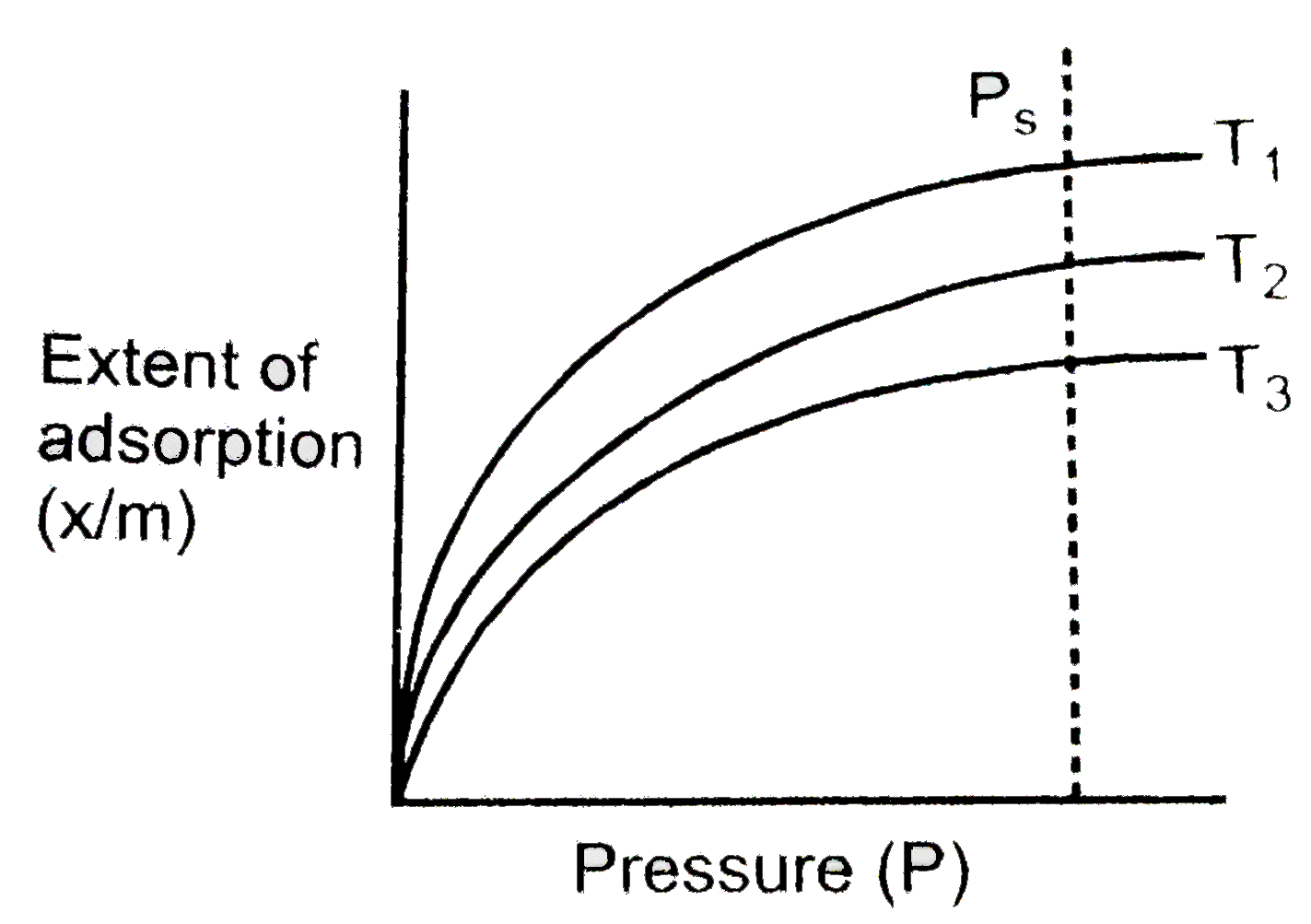
View SolutionFor reaction A rarr B , the rate constant K_(1)=A_(1)(e^(-E_(a_(1))//RT)) and the reaction X rarr Y , the rate constant K_(2)=A_(2)(e^(-E_(a_(2))//RT)) . If A_(1)=10^(9) , A_(2)=10^(10) and E_(a_(1)) =1200 cal/mol and E_(a_(2)) =1800 cal/mol , then the temperature at which K_(1)=K_(2) is : (Given , R=2 cal/K-mol)
View SolutionFor reaction A→B, the rate constant k1=A−Ea1/(RT)1 and for the reactio X→Y, the rate constant k2=A−Ea1/(RT)2 . If A1=108,A2=1010 and Ea1=600 cal /mol, Ea2=1800 cal/mol then the temperature at which k1=k2 is (Given :R=2 cal/K-mol)
View SolutionA reaction takes place in three steps with individual rate constant and activation energy,
Rate constantActivation energyStep 1k1Ea1=180kJ/molStep2k2Ea2=180kJ/molStep3k3Ea3=180kJ/mol
oveall rate constant, k=(k1k2k3)2/3 overall activation energy of the reaction will be :
View SolutionFor reaction A→B, the rate constant k1=A1e−Ea/RT and for the reaction P→Q, the rate constant k2=A2e−Ea2/RT. If A1=108,andEa1=600cal/mol,Ea2=1200cal/mol, then the temperature at which k1=k2 is (R=2cal/K-mol)
View SolutionRate of two reaction whose rate constants are k_(1)& k_(2) are equal at 300 k such that: So caculate n(A_(2))/(A_(1))=?" "Ea_(2)=Ea_(1)=2RT.
View SolutionLet, Ck=nCk for0≤k≤nandAk=[C2k−100C2k] for
k≥land
A1+A2+A3+...+An=[k100k2], then
View SolutionA reacation takes place in three steps with actiation energy Ea1=180 KJ/mol , Ea2 =80 KJ/mol , Ea3=50 KJ/mol respectively overall rate constant of the reaction is k=[k1k2k3]2/3 the overall activation energy of reaction will be (Here k1,k2aandk3 are rate constant of first, second and third step respectively.):
View SolutionThe decomposition of ethane follows the rate law (-d[CH_(3)CH_(3)])/(dt)=K[C_(2)H_(6)] with overall K= ((K_(1)K_(2)K_(3)K_(4))/(K_(5))) , where K_(1),K_(2),K_(3),K_(4),K_(5) are the rate constants of various elementary steps.The values of E_(a) of elementary reactions were found to be E_(a_(1))=350(kJ)/(mol ) E_(a_(2))=2 (kJ)/(mol) E_(a_(3))=160(kJ)/(mol) E_(a_(4))=30(kJ)/(mol) , E_(a_(5))=10(kJ)/(mol) The activation energy of the overall reaction is xkJ/mol. The value of (x)/(5) is
View SolutionFor reaction A → B , the rate constant K1=A1(e−Ea1/RT) and the reaction X→Y , the rate constant K2=A2(e−Ea2/RT) . If A1=109, A2=1010 and Ea1=1200 cal/mol and Ea2 =1800 cal/mol , then the temperature at which K1=K2 is : (Given , R=2 cal/K-mol)
View SolutionFor reaction A→B the rate constant k1=A1e−Ea1/RT and for the reaction P→Q the rate constant k2=A2e−Ea2/RT. If A1=108,A2=1010 and Ea1=600,Ea2=1200, then the temperature at which k1=k2 is
View SolutionA chemical reaction occurs in three paths having rate constants k_(1),k_(2) and k_(3) respectively. If Ea_(1),Ea_(2) and E_(a_(3) are 4,5 and 8kJ respectivel and overall rate constant k=(k_(1)k_(3))/(k_(2)) . Assuming A_(av)=(A_(1)A_(3))/(A_(2)) the overall energy of activation in kJ is __________
View Solution
