If M is the mid point of hypotenuse AC of rt. ΔABC then BM=12.....Solution in Punjabi
AC
AB
BC
None.
Step by step video & image solution for If M is the mid point of hypotenuse AC of rt. DeltaABC then BM = 1/2..... by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of Rs 10 per m2 is Rs 15000, find the height of the hall.
View SolutionABC is a right angled triangle with /_B= 90^@. M is the mid-point of AC and BM =sqrt117 .Sum of the length of other two sides AB and BC is 30. Then the value of 1/12 area of DeltaABC] is:
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View SolutionA (3,0,−1),B(2,10,6) and (1,2,1) are the vertices of a triangle. M is the mid point of the line segment joining AC and G is a point on line segment BM dividing 2:1 ratio internally find cos(∠GOA)
View SolutionIn ΔABC,∠B=90∘. If P is the mid-point of side AC, then
PA=PB=
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View SolutionIn ΔABC, ∠B=90∘. D is the midpoint of hypotenuse AC. If BD=4.5cm, then find the length of hypotenuse AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
D is the mid-point of AC
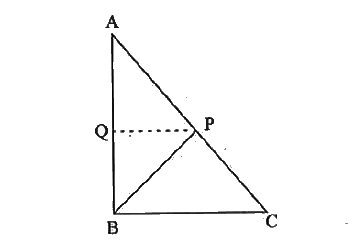
View Solutionयदि M समकोण ΔABC के कर्ण AC का मध्य बिंदु हो तो BM=12……………..
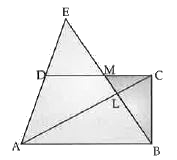
View SolutionThrought the mid-point M of the sides of a parallelogram ABCD, the line BM is drawn intersecting AC at L, and AD produced to E. Prove that EL=2BL.
View SolutionIf M is the mid point of hypotenuse AC of rt. ΔABC then BM=12.....
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that MD⊥AC.
View SolutionIn the adjoining figure, BM and CN are the altitudes drawn to the sides AC and AB respectively of ΔABC. If BM=CN, prove that ΔABC is isosceles.

View SolutionABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View SolutionIn ΔABC,BM⊥ACandCN⊥AB, show that :
ABAC=BMCN=AMAN
View Solution
