Prove that chords of the same length in a circle are at the same distance from the centre.Solution in Malayalam
Step by step video & image solution for Prove that chords of the same length in a circle are at the same distance from the centre. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that the.circumcentre of an equilateral triangle is the same as its centroid.
i) Calculate the length of a side. of an equilateral triangle with vertices on a circle of diameter 1 ceritimetre.
ii). Calculate the perimeter of such a triạngle.
View SolutionWrite the fractions below in decimal form:
(i) frac 3\20
(ii)frac 3\40
(iii) 13\40
(iv)frac 7\80
(v) frac 5\16
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
View SolutionThe length of two parallel chords of a circle are 6cm and 8cm. If the smaller chord is at a distance of 4cm from the centre, what is the distance of the other chord from the centre?
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre?
View SolutionProve that the chords inclined on the same angle to the radius or diameter of a circle are equal in length.
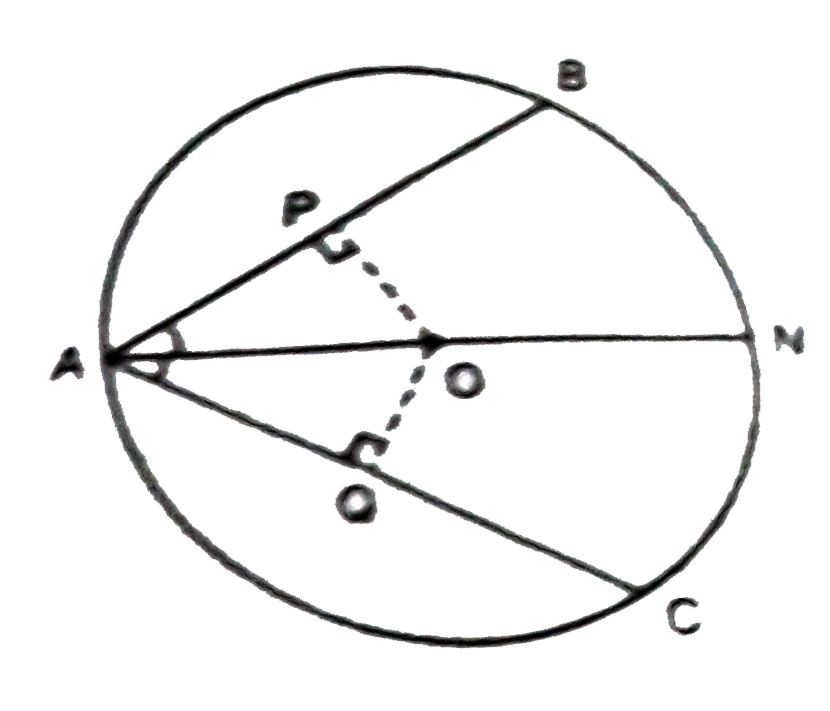
View SolutionThe radius of a circle with centere P is 25 cm . The length of a chord of the same circle is 48 cm . Find the distance of the chord from the centre P of the circle.
View SolutionIf the length of a chord of a circle is 48 cm and the distance of this chord from the centre is 7 cm , then find the length of the chord , the distance of which form the centre is 20 cm.
View SolutionProve that between two chords of a circle, the chord which is at a greater distance form the centre is lesser in length than the chord which is at a closer distance form the centre.
View SolutionIf the length of a chord of a circle at a distance of 24 cm from the centre of a circle is 36 cm, find the length of the greatest chord of the circle.
View SolutionProve that chords of the same length in a circle are at the same distance from the center.
View SolutionA chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
View SolutionProve that the chords inclined on the same angle to the radius or diameter of a circle are equal in length.

View SolutionLength of radius and length of one chord of a circle are 13 cm and 10cm respectively. The distance from centre to the chord of the circle is.
View SolutionThe length of diameter in a circle is 10 cm. If the distance from centre to chord of this circle is 4 cm, then find the length of this chord.
View Solution
