Draw a right triangle and the perpendicular from the midpoint of the hypotenuse to the base.
i) Prove that this perpendicular is half the perpendicular side of the large triangle.
ii) Prove that this perpendieular bisects the bottom side of the larger triangle.
iiii) Prove that in the large triangle, the distances from the midpoint of the hypoteniuse to all the vertices are equal.
iv) Prove thàt the circumcentre of a right triangle is the midpoint of its hypotenuse.Solution in Malayalam
Step by step video & image solution for Draw a right triangle and the perpendicular from the midpoint of the hypotenuse to the base.i) Prove that this perpendicular is half the perpendicular side of the large triangle.ii) Prove that this perpendieular bisects the bottom side of the larger triangle.iiii) Prove that in the large triangle, the distances from the midpoint of the hypoteniuse to all the vertices are equal. iv) Prove thàt the circumcentre of a right triangle is the midpoint of its hypotenuse. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
In the picture, the square on the hypotenuse of the top most right triangle Is drawn. Calculate the area and the length of a side of the square.
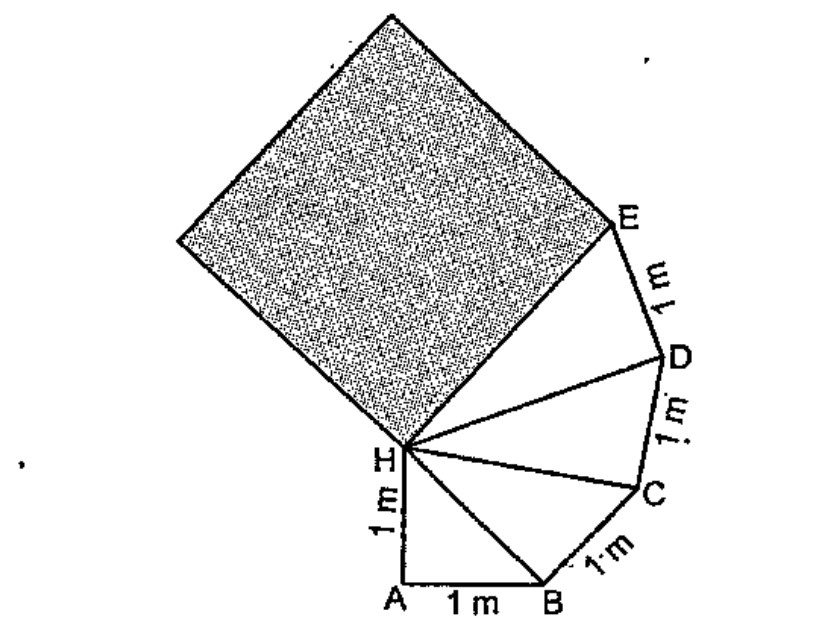 .07:04View Solution
.07:04View SolutionIn rectangle with one side 1cm shorter than the other , take the length of the shorter side as x cm.
i) Taking their perimeters as p(x) cm, write the relation between p(x) and x as an equation.
ii) Taking their areas as a(x) sq.cm, write the relation between a(x) and x as an equation.
iii) Calculate p(1),p(2),p(3),p(4),p(5). Do you see any pattern?
iv) Calculate a(1),a(2),a(3),a(4),a(5).Do you see any pattern?05:56View SolutionIf a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
05:04View SolutionProve that the perpendicular let fall from the vertices of a triangle to the opposite sides are concurrent.
05:04View Solutionसिद्ध कीजिए कि त्रिभुज की शीर्षों से सम्मुख भुजाओं पर डाले गये लम्ब संगामी होते हैं |
03:37View Solutionसिद्ध कीजिए कि त्रिभुज की शीर्षों से सम्मुख भुजाओं पर डाले गये लम्ब संगामी होते हैं |
View Solutionसिद्ध करें कि समद्विबाहु त्रिभुज के शीर्षकोण के अर्द्धक रेखा आधार पर लम्ब होती है और उसे समद्विभाजित करती है |
06:01View Solution(i) साबित करें कि समकोण त्रिभुज मैं कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के
योगफल के बराबर होता है |
(ii) साबित करें कि समकोण त्रिभुज मैं कर्ण का मध्यबिन्दु तीनों शीर्षों से सामान दुरी
पर होता है |06:07View SolutionProve by vector method that the perpendiculars (altitudes) from the vertices to the sides of a triangle are concurrent.
08:36View Solutionযুক্তি দিয়ে প্রমাণ করো, যে-কোনো সমকোণী ত্রিভুজের অতিভুজের মধ্যবিন্দু ত্রিভুজের তিনটি শীর্ষবিন্দু থেকে সমদূরবর্তী ।
08:36View SolutionIf a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
07:07View SolutionIf a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
04:34View Solutionसिद्ध कीजिए कि किसी त्रिभुज की भुजाओं के लम्ब अर्द्धक संगामी होते हैं |
03:30View SolutionDraw a right triangle and the perpendicular from the midpoint of the of the hypotenuse to the base
Prove that this perpendicular is half the perpendicular side of the large triangle.
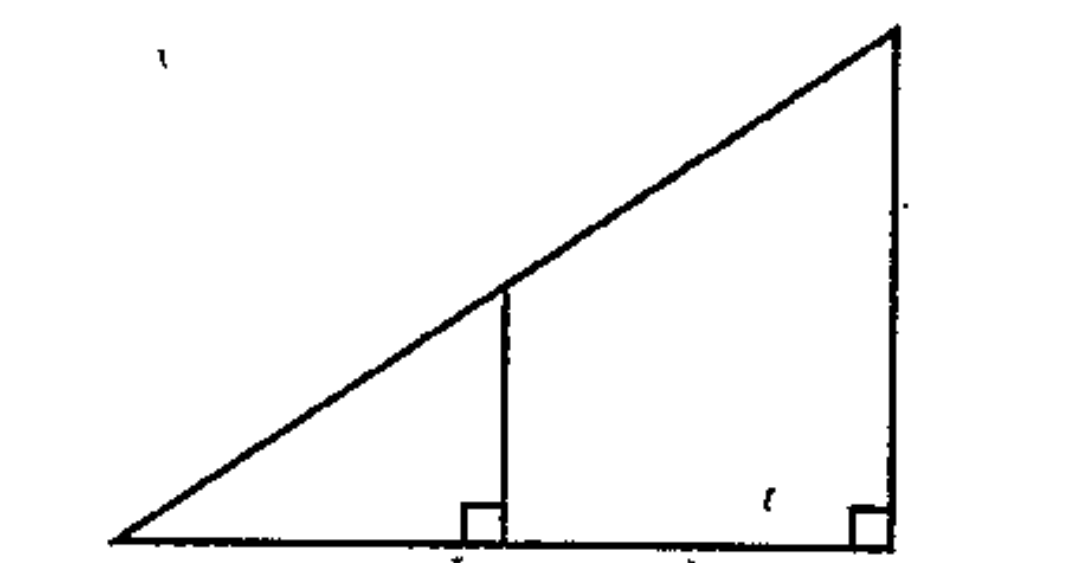 .05:50View Solution
.05:50View SolutionDraw a right triangle and the perpendicular from the midpoint of the of the hypotenuse to the base
Prove that perpendicular bisects the bottom side of the larger triangle.
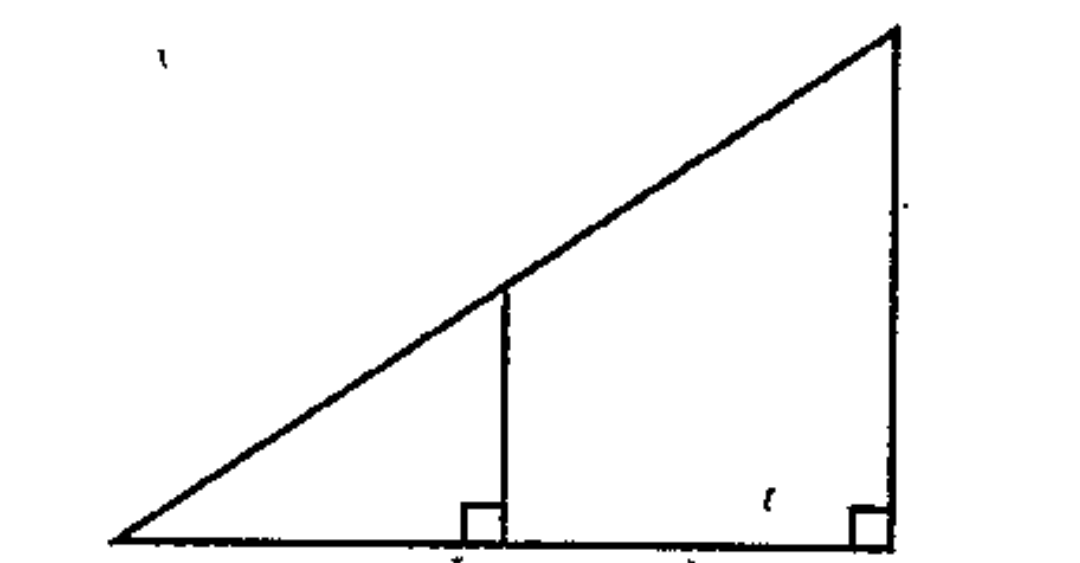 .06:24View Solution
.06:24View SolutionDraw a right triangle and the perpendicular from the midpoint of the of the hypotenuse to the base
Prove that in the large triangle the distances from the midpoint of the hypotenuse to all thevertices are equal.
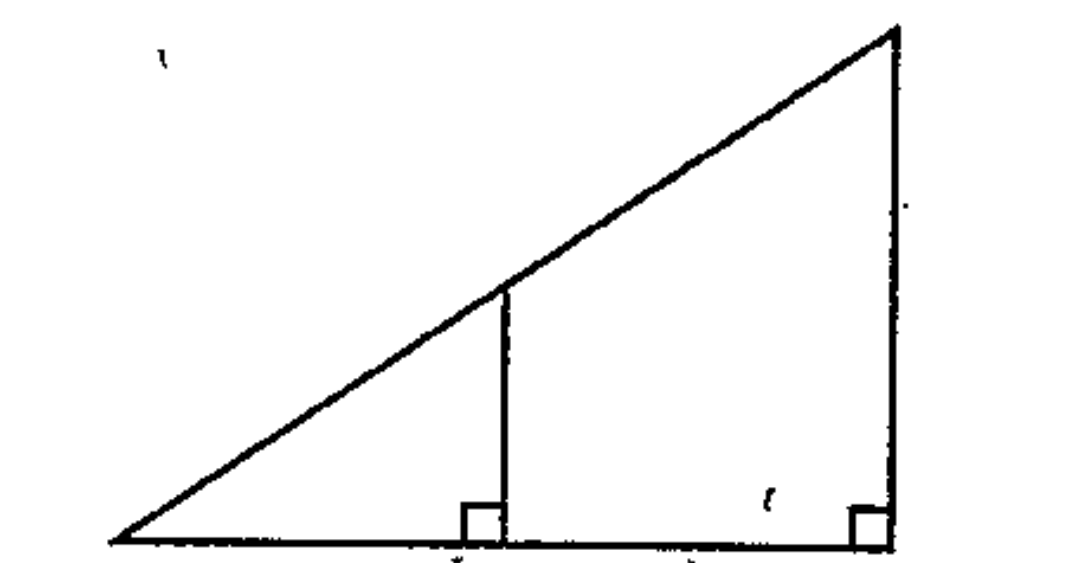 .09:20View Solution
.09:20View Solution
