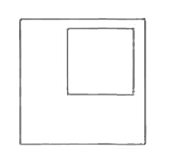
Is there any relation between the side of the large square and some length related to the smaller square?
Length of the large square is the diagonal.of the smaller square.
Similar Questions
Relation between the digit of a perfect square and its square root
View SolutionIn the Figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?
View Solution
Knowledge Check
A square contains four times the area of another square. If one side of the larger square be 4 cm greater than that of smaller square, then the perimeter of smaller square will be equal to
A8 cmB16 cmC24 cmD32 cmThe length of side of a square is 'a' metre. A second square is formed by joining the middle points of this square. Then a third square is formed by joining the middle points of the sides of the second square and so on. Then, the sum of the areas of squares which carried upto infinity, is
Aa2B2a2C3a2D4a2What is the respective ratio between the length of a rectangle and side of a square?
I. Area of the square is 576 sq cm and the area of the rectangle is 600 sq cm
II. Breadth of the rectangle is half the side of the square.AIf the Statement I alone is sufficient to answer the question but the Statement II alone is not sufficientBIf the Statement II alone is sufficient to answer the question but the Statement alone is not sufficientCIf both Statements I and II together are needed to answer the questionDIf either the Statement I alone or Statement II alone is sufficient to answer the question
In the Figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?
View SolutionIf twice the area of a smaller square is subtracted from the area of a larger square, the result is 14cm2. However, if twice the area of the larger square is added to three times the area of the smaller square, the result is 203 cm2 . Determine the sides of the square.
View SolutionIn the figure, the smaller square has sides of length 2 and the larger square has sides of length 4. If a point is chosen at random from the larger square, what is the probability that it will be from the small square?
View SolutionThe length of side of a square is 'a' metre. A second square is formed by joining the middle points of this square. Then a third square is formed by joining the middle points of the sides of the second square and so on. Then, the sum of the areas of squares which carried upto infinity, is
View SolutionThe sum of the areas of two squares is 85. If the sides of both squares have integer lengths, what is the least possible value for the length of a side of the smaller square?
View Solution
