Three brands of pens A, B and Care available in packets of 10, 12 and 24 respectively. If a shopkeeper wants to buy equal number of pens of each brand, what is the minimum number of packets of each brand, he should buy?
A = 10, B = 12, C = 5
A = 5, B = 12, C = 10
A = 10, B = 5C = 12
A = 12, B = 10, C = 5
The correct Answer is:D
To find the minimum number of packets of each brand (A, B, and C) that the shopkeeper should buy to have an equal number of pens, we will follow these steps:
Step 1: Identify the number of pens in each packet
- Brand A has 10 pens per packet.
- Brand B has 12 pens per packet.
- Brand C has 24 pens per packet.
Step 2: Find the Least Common Multiple (LCM) of the packet sizes
To find the minimum number of pens that can be bought equally from all three brands, we need to calculate the LCM of 10, 12, and 24.
- The prime factorization of each number is:
- 10 = 2 × 5
- 12 = 2² × 3
- 24 = 2³ × 3
- The LCM is found by taking the highest power of each prime number:
- For 2: the highest power is 2³ (from 24)
- For 3: the highest power is 3¹ (from 12 and 24)
- For 5: the highest power is 5¹ (from 10)
Thus, the LCM = 2³ × 3¹ × 5¹ = 8 × 3 × 5 = 120.
Step 3: Calculate the number of packets needed for each brand
Now that we have the LCM (120), we can determine how many packets of each brand are needed to reach this total.
- For Brand A:
Number of packets=12010=12 packets
- For Brand B:
Number of packets=12012=10 packets
- For Brand C:
Number of packets=12024=5 packets
Conclusion
The shopkeeper should buy:
- 12 packets of Brand A,
- 10 packets of Brand B,
- 5 packets of Brand C.
- Brand A has 10 pens per packet.
- Brand B has 12 pens per packet.
- Brand C has 24 pens per packet.
To find the minimum number of pens that can be bought equally from all three brands, we need to calculate the LCM of 10, 12, and 24.
- 10 = 2 × 5
- 12 = 2² × 3
- 24 = 2³ × 3
- For 2: the highest power is 2³ (from 24)
- For 3: the highest power is 3¹ (from 12 and 24)
- For 5: the highest power is 5¹ (from 10)
Now that we have the LCM (120), we can determine how many packets of each brand are needed to reach this total.
Number of packets=12010=12 packets
Number of packets=12012=10 packets
Number of packets=12024=5 packets
The shopkeeper should buy:
- 12 packets of Brand A,
- 10 packets of Brand B,
- 5 packets of Brand C.
Similar Questions
Three brands A, B and C of biscuits are available in packets of 12, 15 and 21 biscuits respectively. If a shopkeepeer wants to buy an equal number of biscuits, of each brand, what is the minimum number of packets of each brand, he should buy?
View SolutionThree brands A, B and C of biscuits are available in packets of 12, 15 and 21 biscuits respectively. If a shopkeeper wants to buy an equal number of biscuits, of each brand, what is the minimum number of packets of each brand, he should buy?
View Solution
Knowledge Check
Ram wants to show 15 pictures he took. He wants to put an equal number of pictures on 3 posters. Which number sentence shows how many pictures Ram should put on each poster?
A15÷3=5B15×3=45C15+3=18D15−3=12
Two brands of chocolates are available in packs of 24 and 15 respectively. If I need to buy an equal number of chocolates of both kinds, what is the least number of boxes of each kind I would need to buy?
View SolutionThe largest or greatest among common divisors of two or more integers is called the Greatest Common Divisor (GCD) or Highest Common Factor (H.C.F.)
Two brands of chocolate are available in packs of 24 and 15 respectively. If I need to buy an equal number of chocolates of both kinds, then what is the least number of boxes of each kind I would need to buy?
View Solution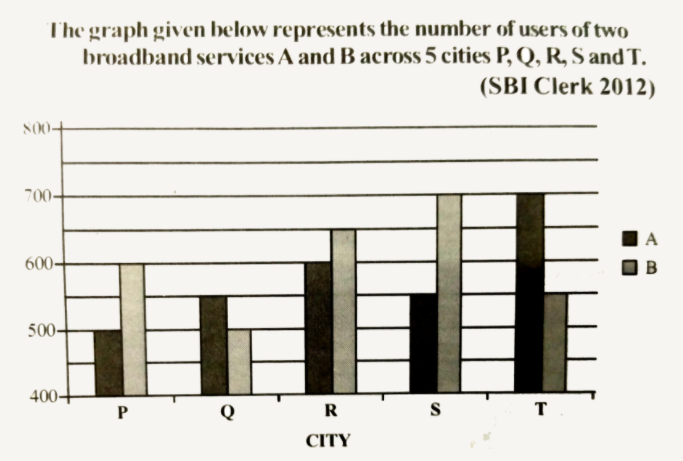
What is the respective ratio of the number of users of brand A in city P to the number of users of brand B in city S ?
View SolutionA farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
View SolutionA farmer mixes two brands P and Q of cattle feed. Brand P costing Rs. 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs. 200 per bag contains 1.5 units of nutritonal element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A,B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
View SolutionIn a school library, there are 780 books of English and 364 books of Science. Ms. Yakang, the librarian of the school wants to store these books in shelves such that each shelf should have the same number of books of each subject. What should be the minimum number of books in each shelf?
View SolutionQuestion #2 Sumit went to the market with Rs. 100. If he buys three pens and six pencils he uses up all his money. On the other hand, if he buys three pencils and six pens he would fall short by 20%. If he wants to buy equal number of pens and pencils, how many pencils can he buy?
View Solution
