For which of the following figures, diagonals are perpendicular to each other?
Parallelogram
Kite
Trapezium
Rectangle
The correct Answer is:B
To determine which of the given figures has diagonals that are perpendicular to each other, we will analyze each figure step by step.
1. Identify the Figures:
We need to consider the following figures: Parallelogram, Trapezium, Rectangle, and Kite.
2. Analyze the Parallelogram:
- In a parallelogram, the diagonals bisect each other.
- However, they do not intersect at right angles (90 degrees).
- Conclusion: The diagonals of a parallelogram are not perpendicular.
3. Analyze the Trapezium:
- In a trapezium, the diagonals do not bisect each other.
- They also do not intersect at right angles.
- Conclusion: The diagonals of a trapezium are not perpendicular.
4. Analyze the Rectangle:
- In a rectangle, the diagonals bisect each other and are equal in length.
- However, they do not intersect at right angles.
- Conclusion: The diagonals of a rectangle are not perpendicular.
5. Analyze the Kite:
- In a kite, one diagonal bisects the other.
- The diagonals of a kite intersect at right angles (90 degrees).
- To prove this, consider the two triangles formed by the diagonals. The sides of the kite are equal, and the angles formed at the intersection are congruent due to the properties of isosceles triangles.
- Conclusion: The diagonals of a kite are perpendicular to each other.
Final Answer:
The figure for which the diagonals are perpendicular to each other is the Kite.
---
We need to consider the following figures: Parallelogram, Trapezium, Rectangle, and Kite.
- In a parallelogram, the diagonals bisect each other.
- However, they do not intersect at right angles (90 degrees).
- Conclusion: The diagonals of a parallelogram are not perpendicular.
- In a trapezium, the diagonals do not bisect each other.
- They also do not intersect at right angles.
- Conclusion: The diagonals of a trapezium are not perpendicular.
- In a rectangle, the diagonals bisect each other and are equal in length.
- However, they do not intersect at right angles.
- Conclusion: The diagonals of a rectangle are not perpendicular.
- In a kite, one diagonal bisects the other.
- The diagonals of a kite intersect at right angles (90 degrees).
- To prove this, consider the two triangles formed by the diagonals. The sides of the kite are equal, and the angles formed at the intersection are congruent due to the properties of isosceles triangles.
- Conclusion: The diagonals of a kite are perpendicular to each other.
The figure for which the diagonals are perpendicular to each other is the Kite.
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - APPLICATIONS, GAMES AND PUZZLES
3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
Similar Questions
Knowledge Check
In which of the following figures are the diagonals equal ?
AParallelogramBRhombusCTrapeziumDRectangleWhat will be the magnitude of electric field at point O as shown in figure ? Each side of the figure is l and perpendicular to each other ?
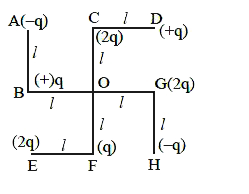 A14πε0ql2B14πε0q(2l2)(2√2−1)Cq4πε0(2l)2D14πε02q2l2(√2)
A14πε0ql2B14πε0q(2l2)(2√2−1)Cq4πε0(2l)2D14πε02q2l2(√2)Which of the following molecular orbital has two nodal planes perpendicular to each other?
Aσ2sBπpxCπ∗2pyDσ∗2pz
Diagonals of a rectangle are perpendicular to each other.
View SolutionShow that the diagonals of a rhombus are perpendicular to each other
View SolutionTwo equal electric currents are flowing perpendicular to each other as shown in the figure. AB and CD are perpendicular to each other and symmetrically placed with respect to the current flow. Where do we expect the resultant magnetic field to be zero?

View SolutionWrite the converse statement of the following statement : If a quadrilateral is a rhombus then its diagonals are perpendicular bisectors of each other . Also state whether the converse statement is true .
View SolutionWhich of the following statements are true and which are false ?
The diagonals of a rectangle are perpendicular to each other .
View Solution
