In the figure, BEST is a rhombus, Then the value of y – x is
40°
50°
20°
10°
To find the value of y−x in the rhombus BEST, we can follow these steps:
Step 1: Identify the Angles
In the rhombus BEST, we know that:
- Angle X is at vertex O (angle OTS).
- Angle Y is at vertex E (angle SOE).
- The angle OBE is given as 40∘.
Step 2: Use Properties of Rhombus
Since BEST is a rhombus, opposite angles are equal and the diagonals bisect each other at right angles. Therefore:
- Angle OBE (which is X) is equal to angle TSO (which is also 40∘).
Step 3: Determine Angle Y
The diagonals of a rhombus intersect at 90∘. Therefore:
- Angle SOE (which is Y) is 90∘.
Step 4: Apply the Exterior Angle Property
In triangle TOS:
- The exterior angle SOE is equal to the sum of the two opposite interior angles OTS and TSO.
- Thus, we can write the equation:
X+40∘=90∘
Step 5: Solve for X
Rearranging the equation gives:
X=90∘−40∘=50∘
Step 6: Calculate Y - X
Now that we have both angles:
- Y=90∘
- X=50∘
We can find y−x:
y−x=90∘−50∘=40∘
Final Answer
The value of y−x is 40∘.
---
In the rhombus BEST, we know that:
- Angle X is at vertex O (angle OTS).
- Angle Y is at vertex E (angle SOE).
- The angle OBE is given as 40∘.
Since BEST is a rhombus, opposite angles are equal and the diagonals bisect each other at right angles. Therefore:
- Angle OBE (which is X) is equal to angle TSO (which is also 40∘).
The diagonals of a rhombus intersect at 90∘. Therefore:
- Angle SOE (which is Y) is 90∘.
In triangle TOS:
- The exterior angle SOE is equal to the sum of the two opposite interior angles OTS and TSO.
- Thus, we can write the equation:
X+40∘=90∘
Rearranging the equation gives:
X=90∘−40∘=50∘
Now that we have both angles:
- Y=90∘
- X=50∘
y−x=90∘−50∘=40∘
The value of y−x is 40∘.
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - APPLICATIONS, GAMES AND PUZZLES
3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
Similar Questions
Knowledge Check
In the given figure PQRS is a rhombus, then the value of x is
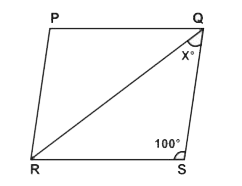 A40∘B50∘C60∘D80∘
A40∘B50∘C60∘D80∘
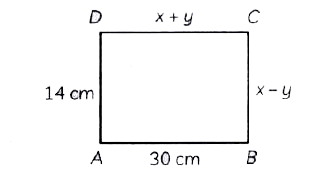
In the given figure ABCD is a parallelogram. Then the values of x and y respectively are

View SolutionIn the given figure, if ABCD is a parallelogram, then the value of 2x +y is equal to ____ degrees.

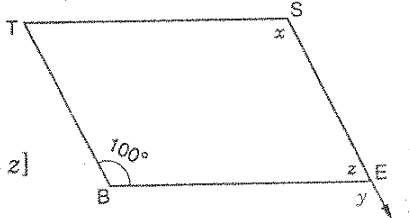
View SolutionIn Figure, BEST is a parallelogram. Find the values of x, y and z.
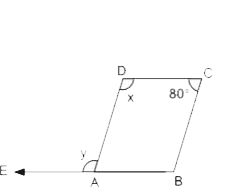
View SolutionIn the figure, ABCD is a parallelogram find value of (x+y).
View SolutionIn the figure if PQRS is a parallelogram, then find the value of x & y.

View SolutionIn the figure given alongside ,find the values of x and y.
View SolutionIn the given figure RICE is a rhombus. Find x+y+z

View Solution