In an equilateral triangle ABC (Fig. 6.2), AD is an altitude. Then 4AD2 is equal to
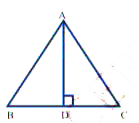
2BD2
BC2
3AB2
2DC2
The correct Answer is:C
Step by step video & image solution for In an equilateral triangle ABC (Fig. 6.2), AD is an altitude. Then 4AD^2 is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In an equilateral ΔABCif AD⊥BC, then
A2AB2=3AD2B3AB2=4AD2C5AB2=6AD2D4AB2=5AD2ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Aa√3Ba√2C2a√3DNoneIn an equilateral triangle ABC, the side BC is trisected at D. Find the value of AD2 :
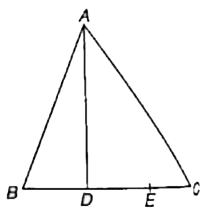 A97AB2B79AB2C34AB2D45AB2
A97AB2B79AB2C34AB2D45AB2
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that Area ( triangle ADE ): Area ( triangle ABC )=3:4.
View SolutionIn the equilateral triangle ABC, AD=DE=BE, D and E lie on the AB. If each side of the △ABC is 6cm ,then the area of the shaded region is
View SolutionIn acute angled triangle ABC,AD is the altitude. Circle drawn with AD as its diameter cuts ABandACatPandQ, respectively. Length of PQ is equal to /(2R) (b) abc4R2 2RsinAsinBsinC (d) /R
View SolutionIn a ΔABC,B=π8andC=5π8 and the altitude AD=h. Then h : a is equal to
View SolutionLet ABC be an equilateral triangle. Let BE⊥CA meeting CA at E, then (AB2+BC2+CA2) is equal to :
View Solution
