Two perpendiculars can be drawn to a given line from a point not lying on it.
To solve the question "Can two perpendiculars be drawn to a given line from a point not lying on it?", we can follow these steps:
1. Understanding Perpendicular Lines:
A perpendicular line is one that intersects another line at a right angle (90 degrees).
Hint: Remember that perpendicular lines create a right angle at the point of intersection.
2. Identifying the Given Elements:
We have a line (let's call it line L) and a point (let's call it point P) that is not on line L.
Hint: Visualize or sketch line L and point P to better understand their positions relative to each other.
3. Drawing the Perpendicular:
From point P, we can draw a line that intersects line L at a right angle. This line is the first perpendicular line.
Hint: Use a protractor or a right-angle tool to ensure that the angle formed is exactly 90 degrees.
4. Considering Other Perpendiculars:
Now, if we try to draw another perpendicular line from point P to line L, we realize that there can only be one unique point of intersection where the perpendicular line meets line L.
Hint: Think about the definition of perpendicularity; if there were two perpendiculars, they would have to intersect line L at two different points, which is not possible.
5. Conclusion:
Therefore, it is not possible to draw two perpendiculars from point P to line L. Only one perpendicular can be drawn from a point not lying on the line.
Hint: Summarize your findings: Only one perpendicular can be drawn from a point to a line.
Final Answer:
Only one perpendicular can be drawn to a given line from a point not lying on it. Hence, the statement is false.
A perpendicular line is one that intersects another line at a right angle (90 degrees).
We have a line (let's call it line L) and a point (let's call it point P) that is not on line L.
From point P, we can draw a line that intersects line L at a right angle. This line is the first perpendicular line.
Now, if we try to draw another perpendicular line from point P to line L, we realize that there can only be one unique point of intersection where the perpendicular line meets line L.
Therefore, it is not possible to draw two perpendiculars from point P to line L. Only one perpendicular can be drawn from a point not lying on the line.
Only one perpendicular can be drawn to a given line from a point not lying on it. Hence, the statement is false.
Topper's Solved these Questions
- SYMMETRY AND PRACTICAL GEOMETRY BOOK - NCERT EXEMPLARCHAPTER - SYMMETRY AND PRACTICAL GEOMETRY EXERCISE - Exercise
29 Videos
- SYMMETRY AND PRACTICAL GEOMETRY BOOK - NCERT EXEMPLARCHAPTER - SYMMETRY AND PRACTICAL GEOMETRY EXERCISE - Exercise (In questions 18 to 42, fill in the blanks to make the statements true.)
25 Videos
- RATIO AND PROPORTIONBOOK - NCERT EXEMPLARCHAPTER - RATIO AND PROPORTIONEXERCISE - Exercise (In questions 35 to 46, fill in the blanks to make the statements true.)
11 Videos
Similar Questions
All the line segment that can be drawn to a given line; from a point;not lying on it; the perpendicular line segment is the shortest.
View SolutionOf all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest. GIVEN : A straight line l and a point P not lying on l. PM⊥l and N is any point on 1 other than M. TO PROVE : PM<PN
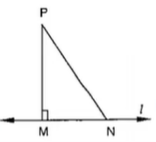
View Solution
Knowledge Check
How many peprndiculars can be drawn to a given line passing through given point not lying on it ?
A0B1C2DinfiniteIf a perpendicular is drawn to a line segment MN at N and point P is marked on perpendicular, then
A¯¯¯¯¯¯¯MP⊥¯¯¯¯¯¯NPB¯¯¯¯¯¯¯¯MN∣∣¯¯¯¯¯¯NPC¯¯¯¯¯¯¯¯MN∣∣¯¯¯¯¯¯¯MPD¯¯¯¯¯¯¯¯MN⊥¯¯¯¯¯¯NP
Infinitely many perpendiculars can be drawn to a given ray.
View SolutionOnly one perpendicular bisector can be drawn to a given line segment.
View SolutionInfinitely many perpendicular bisectors can be drawn to a given ray.
View SolutionHow many lines can be drawn which are perpendicular to a given line and pass through a given point lying (i) outside it? (ii) on it?
View SolutionHow many lines can be drawn through a given point.
View SolutionThere are five points in a plane. From each point, perpendicular are drawn to the lines joining the other points. What is the maximum numbers of points of intersection of these perpendiculars.
View Solution