A set-square and a protractor have the same number of lines of symmetry
To determine whether a 45°, 45°, 90° set-square and a protractor have the same number of lines of symmetry, we can follow these steps:
1. Understand Lines of Symmetry:
- A line of symmetry is a line that divides a shape into two identical halves that are mirror images of each other.
2. Draw the 45°, 45°, 90° Set Square:
- The shape of a 45°, 45°, 90° set square is a right triangle where the two angles of 45° are at the base and the right angle (90°) is at the top.
3. Identify Lines of Symmetry in the Set Square:
- For the 45°, 45°, 90° set square, there is one line of symmetry. This line runs vertically from the right angle down to the midpoint of the base, dividing the triangle into two equal halves.
4. Draw the Protractor:
- The protractor is typically shaped like a semicircle with a straight edge at the bottom.
5. Identify Lines of Symmetry in the Protractor:
- The protractor has one line of symmetry as well. This line runs vertically through the center of the semicircle, dividing it into two equal halves.
6. Compare the Lines of Symmetry:
- Both the 45°, 45°, 90° set square and the protractor have one line of symmetry each.
7. Conclusion:
- Therefore, the statement that a 45°, 45°, 90° set square and a protractor have the same number of lines of symmetry is true.
- A line of symmetry is a line that divides a shape into two identical halves that are mirror images of each other.
- The shape of a 45°, 45°, 90° set square is a right triangle where the two angles of 45° are at the base and the right angle (90°) is at the top.
- For the 45°, 45°, 90° set square, there is one line of symmetry. This line runs vertically from the right angle down to the midpoint of the base, dividing the triangle into two equal halves.
- The protractor is typically shaped like a semicircle with a straight edge at the bottom.
- The protractor has one line of symmetry as well. This line runs vertically through the center of the semicircle, dividing it into two equal halves.
- Both the 45°, 45°, 90° set square and the protractor have one line of symmetry each.
- Therefore, the statement that a 45°, 45°, 90° set square and a protractor have the same number of lines of symmetry is true.
Topper's Solved these Questions
- SYMMETRY AND PRACTICAL GEOMETRY BOOK - NCERT EXEMPLARCHAPTER - SYMMETRY AND PRACTICAL GEOMETRY EXERCISE - Exercise
29 Videos
- SYMMETRY AND PRACTICAL GEOMETRY BOOK - NCERT EXEMPLARCHAPTER - SYMMETRY AND PRACTICAL GEOMETRY EXERCISE - Exercise (In questions 18 to 42, fill in the blanks to make the statements true.)
25 Videos
- RATIO AND PROPORTIONBOOK - NCERT EXEMPLARCHAPTER - RATIO AND PROPORTIONEXERCISE - Exercise (In questions 35 to 46, fill in the blanks to make the statements true.)
11 Videos
Similar Questions
Knowledge Check
A square has how many lines of symmetry
Aone line of symmetryBtwo lines of symmetryCthree lines of symmetryDfour lines of symmetry
Read the statements given below and identify the correct option.
(i) A parallelogram has only one line of symmetry.
(ii) A square and a rectangle have the same number of lines of symmetry.
(iii) The diameter of a circle is its line of symmetry.
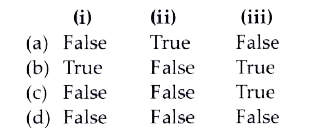
View SolutionThe number of lines of symmetry in a ruler is
View SolutionA protractor has __________ line/lines of symmetry.
View SolutionThe number of lines of symmetry in a circle is
View SolutionA 45∘−45∘−90∘ set - square has _________line / lines of symmetry
View SolutionThe number of lines of symmetry in compasses is
View SolutionThe number of lines of symmetry in a divider is
View Solution

