A stone dropped from a building takes 4 s to reach the ground. The height of the building is
78.4 m
64 m
260 m
2000 m
The correct Answer is:A
x=12gt2
=12×9.8×(4)2
=4×9.8×2
=9.8×8
=78.4 m
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - PHYSICS WALLAHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NEET Past 5 Years Questions
5 Videos
- MOTION IN A STRAIGHT LINEBOOK - PHYSICS WALLAHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NEET Past 5 Years Questions
5 Videos
- MOTION IN A PLANE BOOK - PHYSICS WALLAHCHAPTER - MOTION IN A PLANE EXERCISE - NEET Past 5 years Questions
10 Videos
- MOVING CHARGES AND MAGNETISM BOOK - PHYSICS WALLAHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - NEET PAST 5 YEARS QUESTIONS
12 Videos
Similar Questions
Knowledge Check
A stone is dropped from roof of building takes 5 s to reach the ground. The sound of striking is heard after 5.4 second after the stone is dropped. The velocity of sound is
A312.5ms−1B332.5ms−1C352ms−1D392ms−1A stone dropped from a building takes 4 s to reach the ground. The height of the building is
A78.4 mB64 mC260 mD2000 mA stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
A18.6 mB39.2 mC44.1 mD98 m
A stone falls from a building and reaches the ground 2.5 seconds later. How high is the building? (=9.8m/s2)
View SolutionA body dropped from a height of 5m. Reaches the ground in 1 s. if it takes 2 s to reach the ground , find the height from which it is dropped.
View SolutionA stone is thrown downwards with velocity 10 m/s from the roof of a builng and it reaches the ground with speed 40 m/s. the height of the building would be
View Solutionballoon is rising vertically up with a velocity of 29 m/s. A stone is dropped from it and it reaches the ground in 10 seconds. The height of the balloon when the stone was dropped from it is (g=9.8ms2)
View SolutionThe velocity time graph for the veticaly component of the velocity of a body thrown upwards from the ground and landing on the roof of a building is given in the figure.The height of the building is:
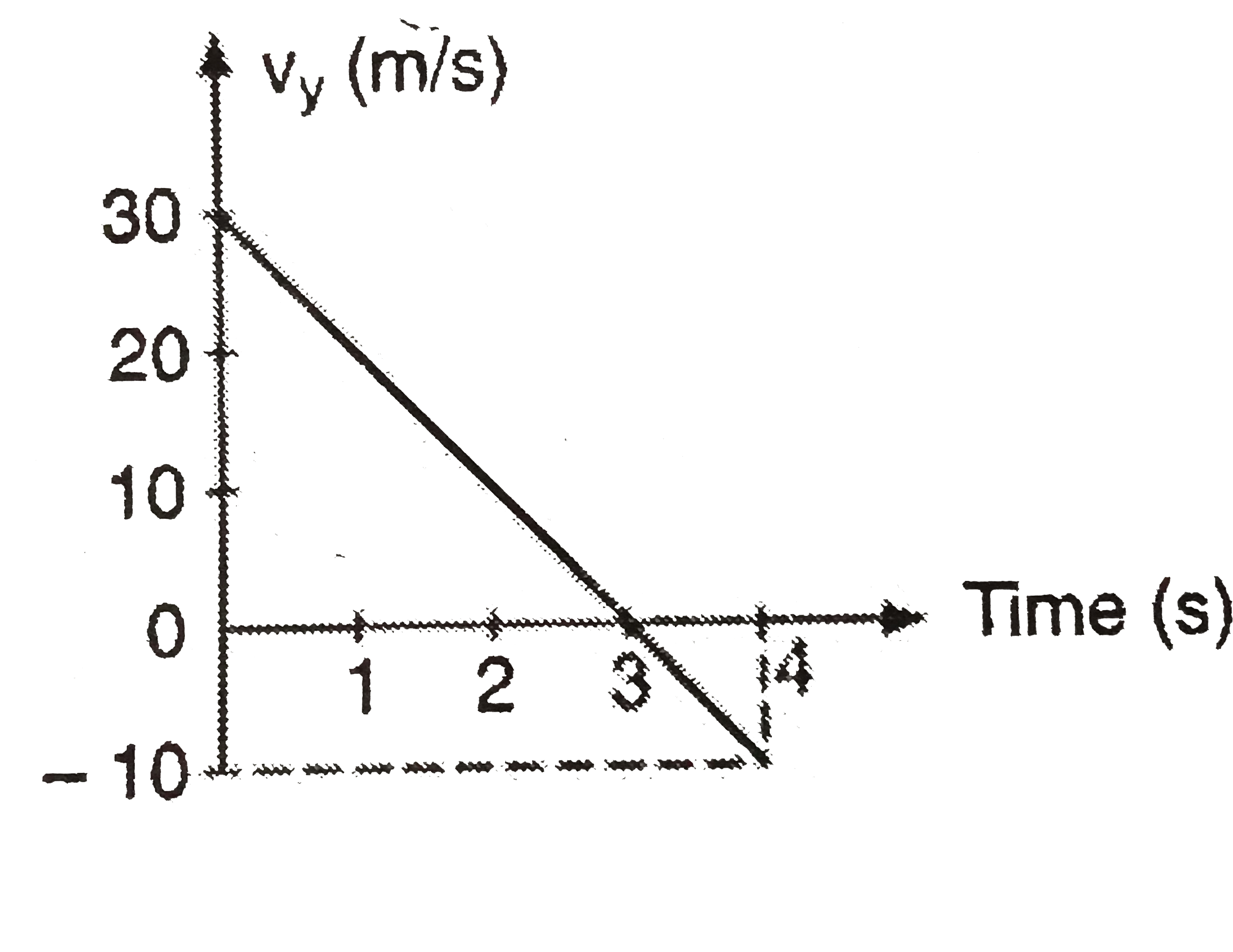
View Solution
