A stone is dropped from the roof of a building takes 4s to reach ground. The height of the building is
19.6m
39.2m
156.8m
78.4m
To find the height of the building from which the stone is dropped, we can use the second equation of motion. Here's a step-by-step solution:
Step 1: Identify the given values
- Time taken (t) = 4 seconds
- Initial velocity (u) = 0 m/s (since the stone is dropped)
- Acceleration (a) = g = 9.8 m/s² (acceleration due to gravity)
Step 2: Write the equation of motion
We will use the second equation of motion:
s=ut+12at2
Step 3: Substitute the known values into the equation
Since the initial velocity u=0, the equation simplifies to:
s=0⋅t+12⋅g⋅t2
s=12⋅9.8⋅(4)2
Step 4: Calculate t2
Calculate t2:
t2=42=16
Step 5: Substitute t2 back into the equation
Now substitute t2 back into the equation:
s=12⋅9.8⋅16
Step 6: Calculate s
Now calculate s:
s=12⋅9.8⋅16=4.9⋅16
s=78.4m
Step 7: Conclusion
The height of the building is 78.4m.
- Time taken (t) = 4 seconds
- Initial velocity (u) = 0 m/s (since the stone is dropped)
- Acceleration (a) = g = 9.8 m/s² (acceleration due to gravity)
We will use the second equation of motion:
s=ut+12at2
Since the initial velocity u=0, the equation simplifies to:
s=0⋅t+12⋅g⋅t2
s=12⋅9.8⋅(4)2
Calculate t2:
t2=42=16
Now substitute t2 back into the equation:
s=12⋅9.8⋅16
Now calculate s:
s=12⋅9.8⋅16=4.9⋅16
s=78.4m
The height of the building is 78.4m.
Similar Questions
Knowledge Check
A stone dropped from a building takes 4 s to reach the ground. The height of the building is
A19.6mB80.4mC78.4mD156.8mA stone is dropped from roof of building takes 5 s to reach the ground. The sound of striking is heard after 5.4 second after the stone is dropped. The velocity of sound is
A312.5ms−1B332.5ms−1C352ms−1D392ms−1A stone dropped from a building takes 4 s to reach the ground. The height of the building is
A78.4 mB64 mC260 mD2000 m
A stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
View SolutionA stone is thrown downwards with velocity 10 m/s from the roof of a builng and it reaches the ground with speed 40 m/s. the height of the building would be
View SolutionThe velocity time graph for the veticaly component of the velocity of a body thrown upwards from the ground and landing on the roof of a building is given in the figure.The height of the building is:
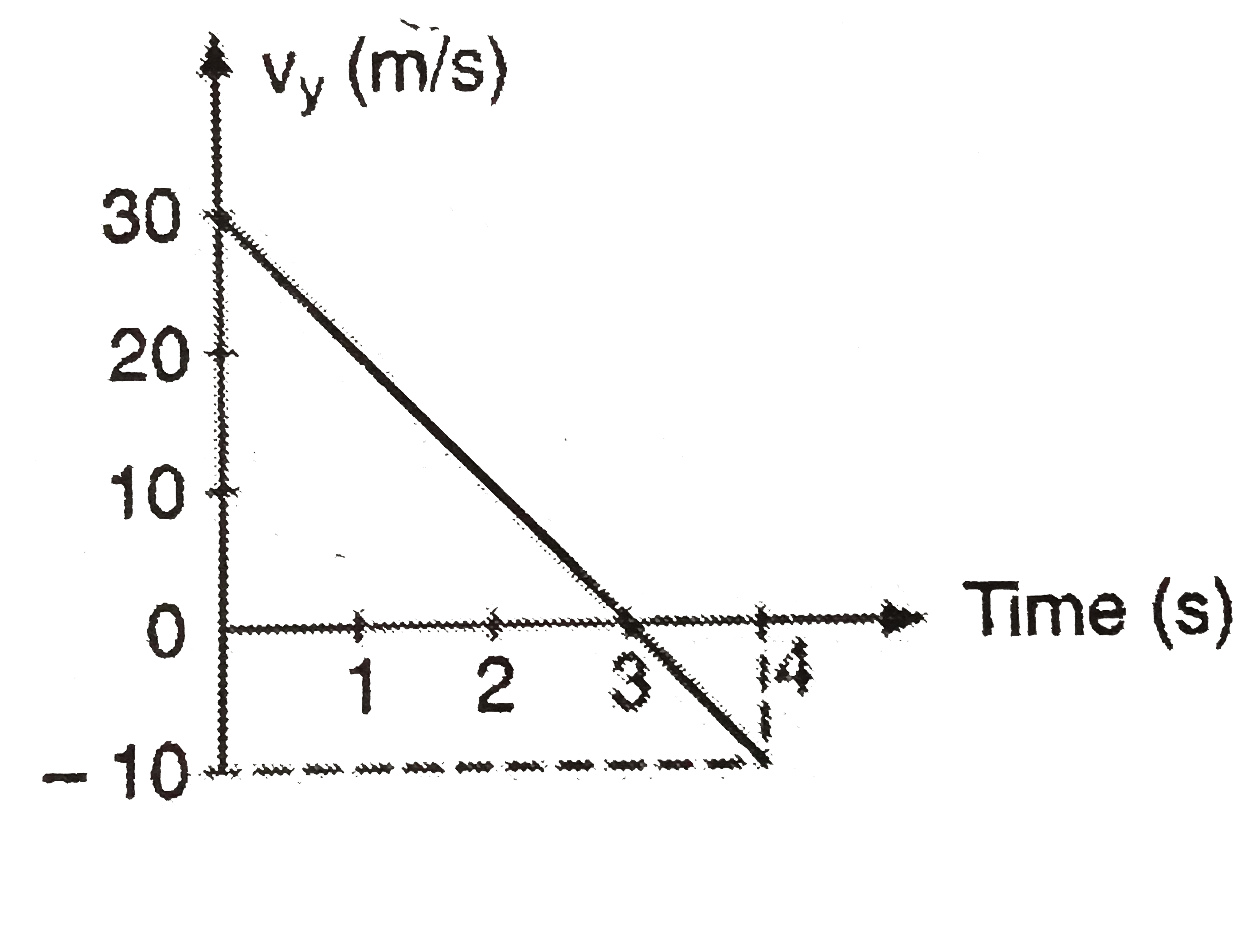
View SolutionThe velocity time graph for the veticaly component of the velocity of a body thrown upwards from the ground and landing on the roof of a building is given in the figure.The height of the building is:
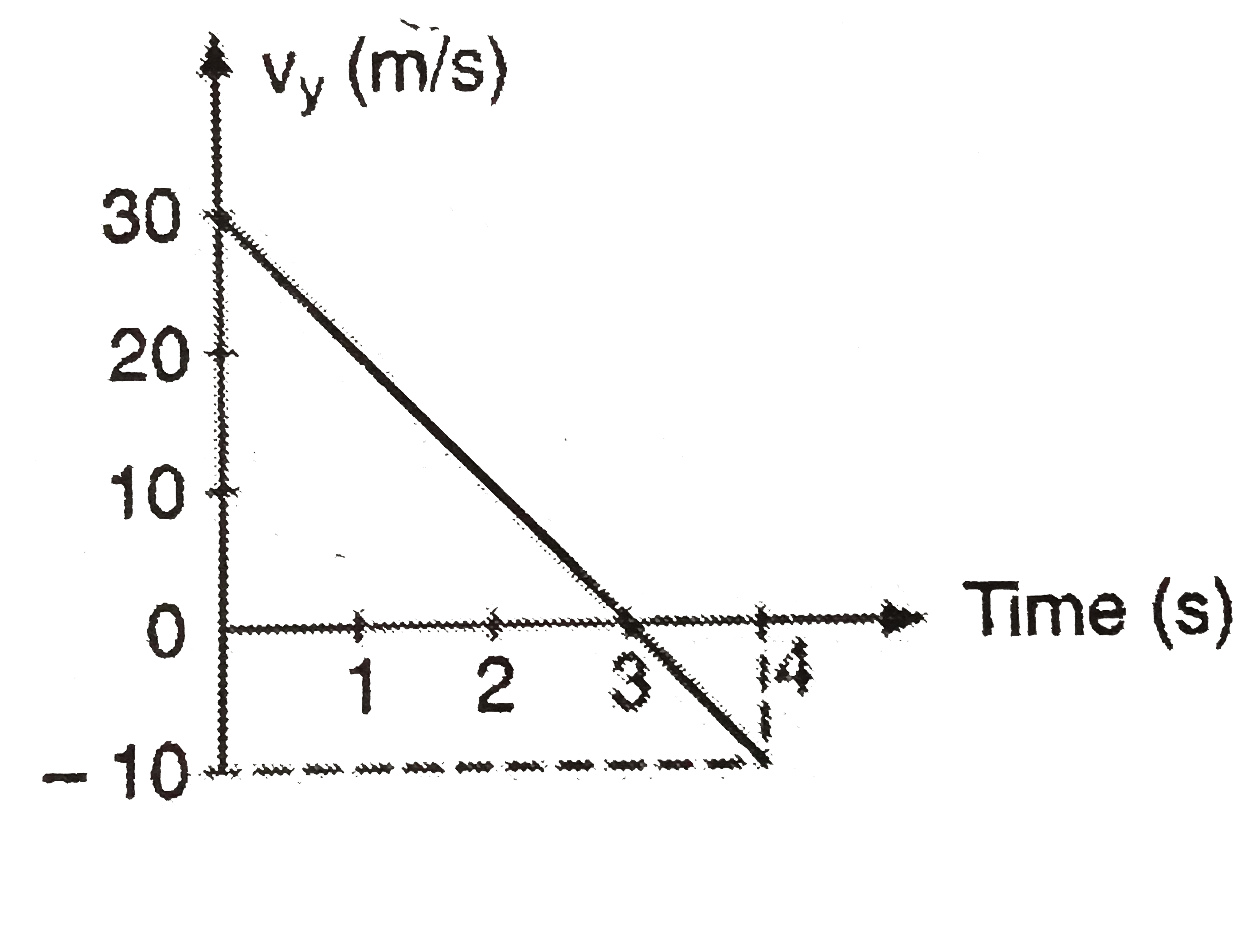
View SolutionA ball dropped from the top of a building takes 0.5 sec to clear the window of 4.9 m height. What is the height of building above the window?
View Solution
