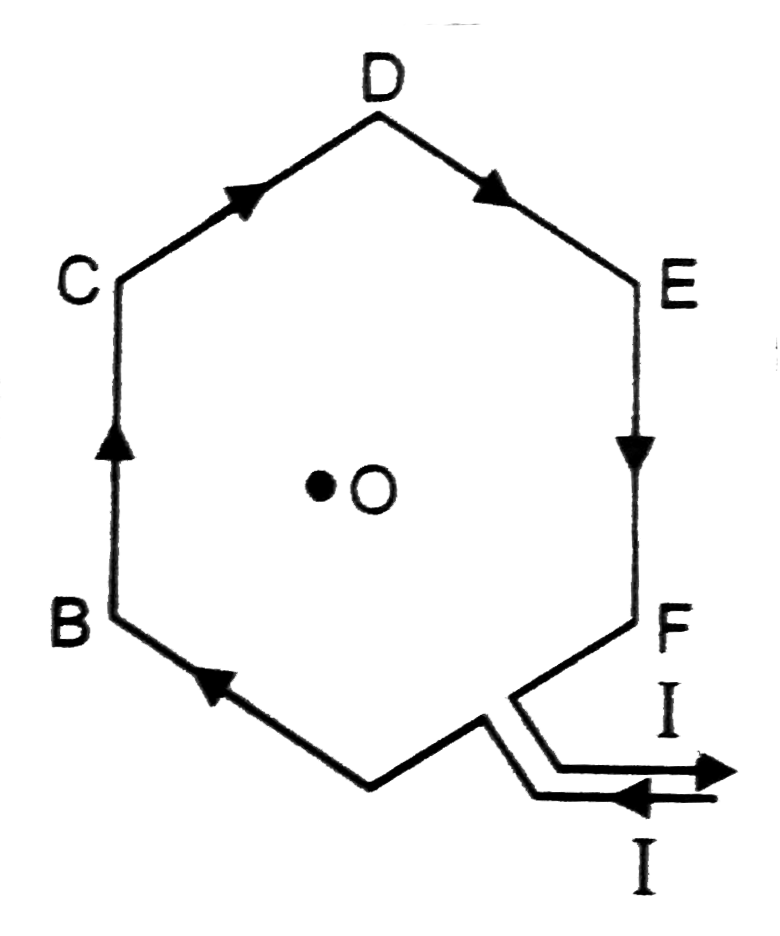
A current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
A
√2μ0Iπa
B
√3μ0Iπa
C
2πa√3I
D
μ0Iπa
Video Solution
Text Solution
The correct Answer is:B
Here ∠EOD=60∘
∠EON=30∘=∠NOD
OE = OD = ED = a
ON=OEcos30∘=a×√32
Total magnetic field induction at O due to current through all the six sides of hexagon is
B=6×μo4π×1a√32(sin30∘+sin30∘)
B=√3μoIπa
|
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - PHYSICS WALLAHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LEVEL - 2
30 Videos
- MOVING CHARGES AND MAGNETISM BOOK - PHYSICS WALLAHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - NEET PAST 5 YEARS QUESTIONS
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - PHYSICS WALLAHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NEET Past 5 Years Questions
5 Videos
- OSCILLATIONS BOOK - PHYSICS WALLAHCHAPTER - OSCILLATIONS EXERCISE - NEET PAST 5 YEARS QUESTIONS
5 Videos
Similar Questions
Knowledge Check
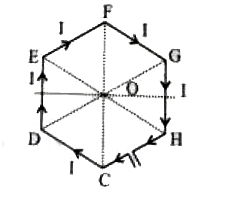
A current I is flowing in an octagonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
 A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πa
A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πaA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
 A√2μ0IπaB√3μ0IπaC2πa√3IDμ0Iπa
A√2μ0IπaB√3μ0IπaC2πa√3IDμ0IπaA current I flows through a closed loop as shown in figure. The magnetic field induction at the centre 0 is
 Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)
Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)
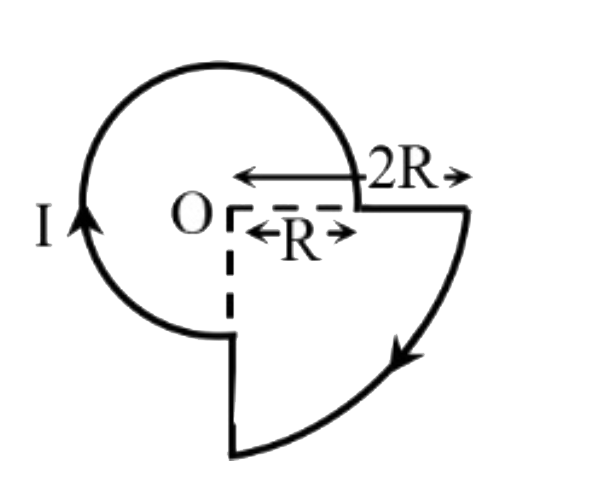
In the net work shown in figure,find the magnetic field at the centre O of the coil.
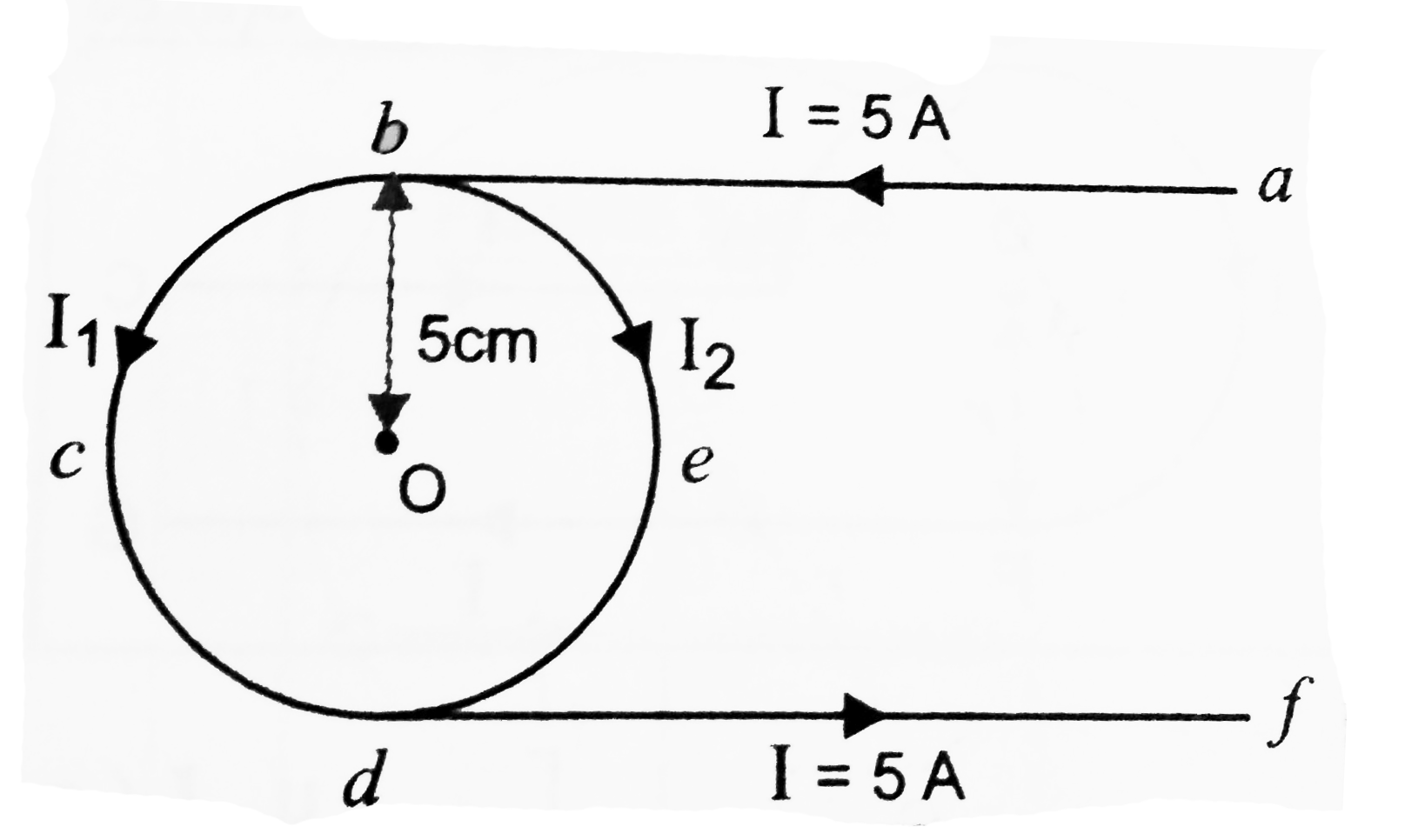
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
View SolutionMagnetic field induction at the centre of a circular coil shown in the figure is
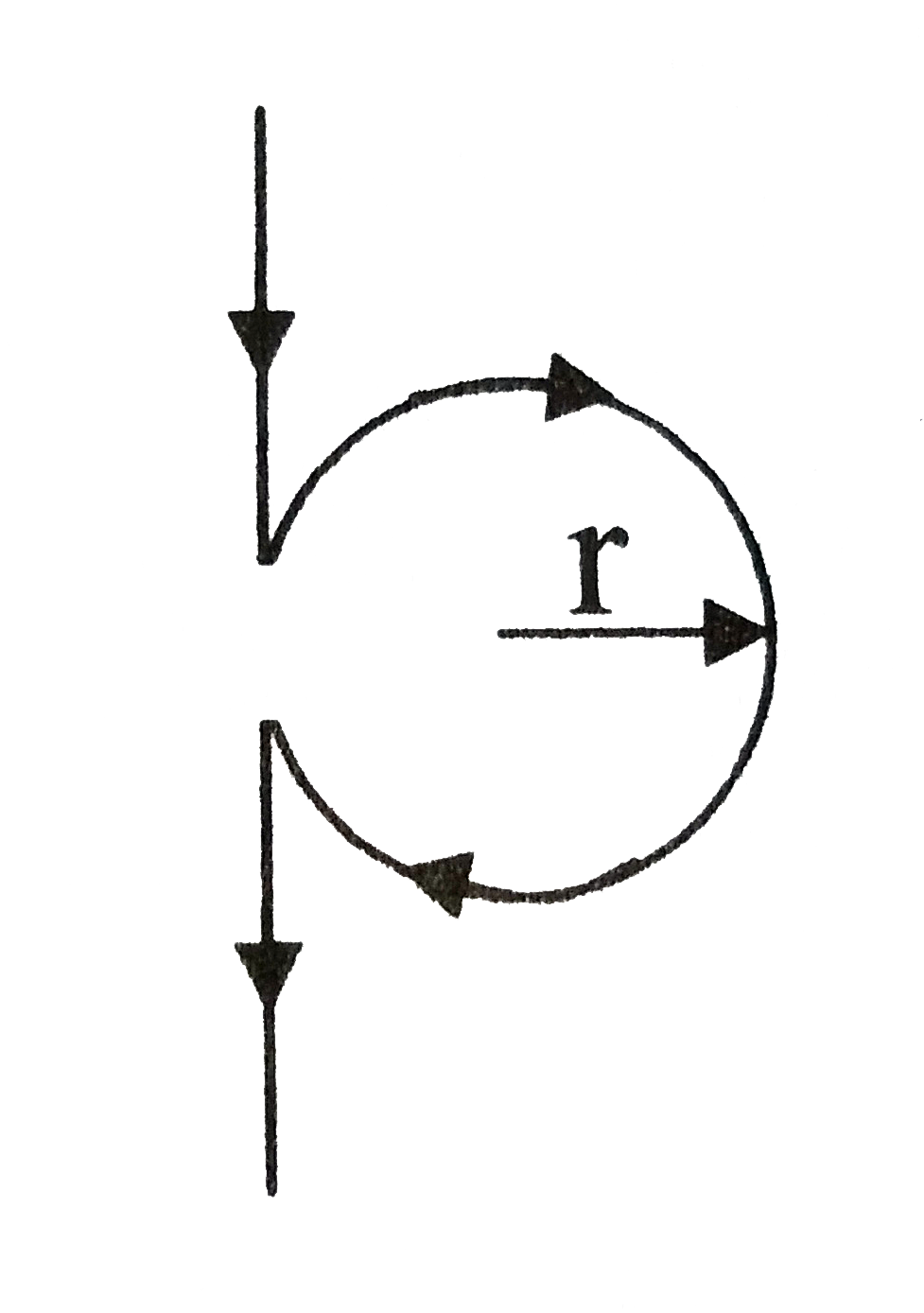
View SolutionThe magnetic field at the centre of current carrying coil is
View SolutionTwo similar coils of radius R are lying concentrically with their planes at right angles to each other. The currents flowing in them are I and 2I, respectively. The resultant magnetic field induction at the centre will be
View Solution
