Current I A flowing in a circular coil of radius r. then the magnetic induction at the centre is B. If the current is doubled then the magnetic induction will be
To solve the problem, we need to determine how the magnetic induction (magnetic field) at the center of a circular coil changes when the current flowing through it is doubled.
1. Understand the Formula for Magnetic Induction:
The magnetic induction (B) at the center of a circular coil carrying current is given by the formula:
B=μ0I2R
where:
- B = magnetic induction at the center,
- μ0 = permeability of free space (a constant),
- I = current flowing through the coil,
- R = radius of the coil.
2. Identify Initial Conditions:
Initially, the current flowing in the coil is I, and the magnetic induction at the center is given as B. Thus, we can express this as:
B=μ0I2R
3. Doubling the Current:
If the current is doubled, the new current I′ becomes:
I′=2I
4. Calculate the New Magnetic Induction:
Substitute I′ into the magnetic induction formula:
B′=μ0I′2R=μ0(2I)2R=2μ0I2R=μ0IR
5. Relate New Magnetic Induction to Initial:
We can relate the new magnetic induction B′ to the initial magnetic induction B:
B′=2⋅μ0I2R=2B
6. Conclusion:
Therefore, when the current is doubled, the new magnetic induction at the center of the coil becomes:
B′=2B
Final Answer:
If the current is doubled, the magnetic induction will be 2B.
The magnetic induction (B) at the center of a circular coil carrying current is given by the formula:
B=μ0I2R
where:
- B = magnetic induction at the center,
- μ0 = permeability of free space (a constant),
- I = current flowing through the coil,
- R = radius of the coil.
Initially, the current flowing in the coil is I, and the magnetic induction at the center is given as B. Thus, we can express this as:
B=μ0I2R
If the current is doubled, the new current I′ becomes:
I′=2I
Substitute I′ into the magnetic induction formula:
B′=μ0I′2R=μ0(2I)2R=2μ0I2R=μ0IR
We can relate the new magnetic induction B′ to the initial magnetic induction B:
B′=2⋅μ0I2R=2B
Therefore, when the current is doubled, the new magnetic induction at the center of the coil becomes:
B′=2B
If the current is doubled, the magnetic induction will be 2B.
Topper's Solved these Questions
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Assignment Problems (Subjective) (Level - II & III)
15 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Assignment Problems (Objective) (LEVEL-I)
50 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Exercise
11 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
- MAGNETISMBOOK - FIITJEECHAPTER - MAGNETISMEXERCISE - Example
12 Videos
Similar Questions
Due to the flow of current in a circular loop of radius "R" ,the magnetic induction produced at the centre of the loop is B and magnetic moment of the coil is M .The value of (B)/(M) will be (mu_(0) is magnetic, permeability
View SolutionWhen a long wire carrying a steady current is best into a circular coil of one turn, the magnetic induction at its centre is B. When the same wire carrying the same current is bent into a circular coil of one turn, the magnetic induction at its centre is B. when the same wire carrying the same current is bent to form a circular coil of a turns of a smaller radius, the magnetic induction at the centre will be
View Solution
Knowledge Check
A current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
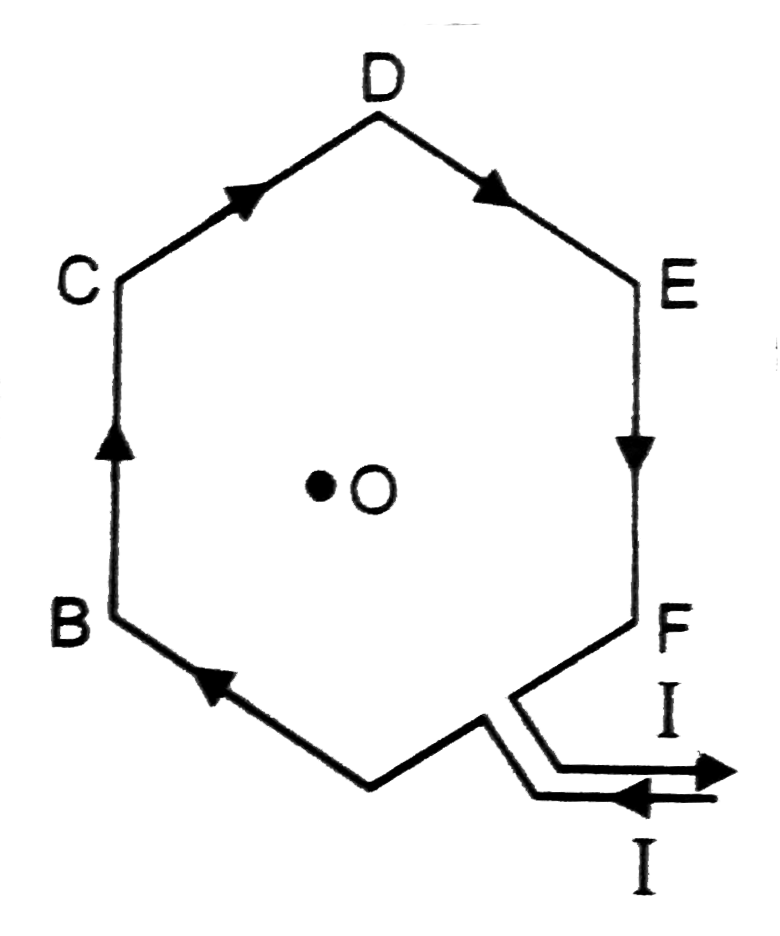 Aμ0I3√3πaB√3μ0IπaC3√3μ0IπaDμ0I√3πa
Aμ0I3√3πaB√3μ0IπaC3√3μ0IπaDμ0I√3πaA current I is flowing in an octagonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
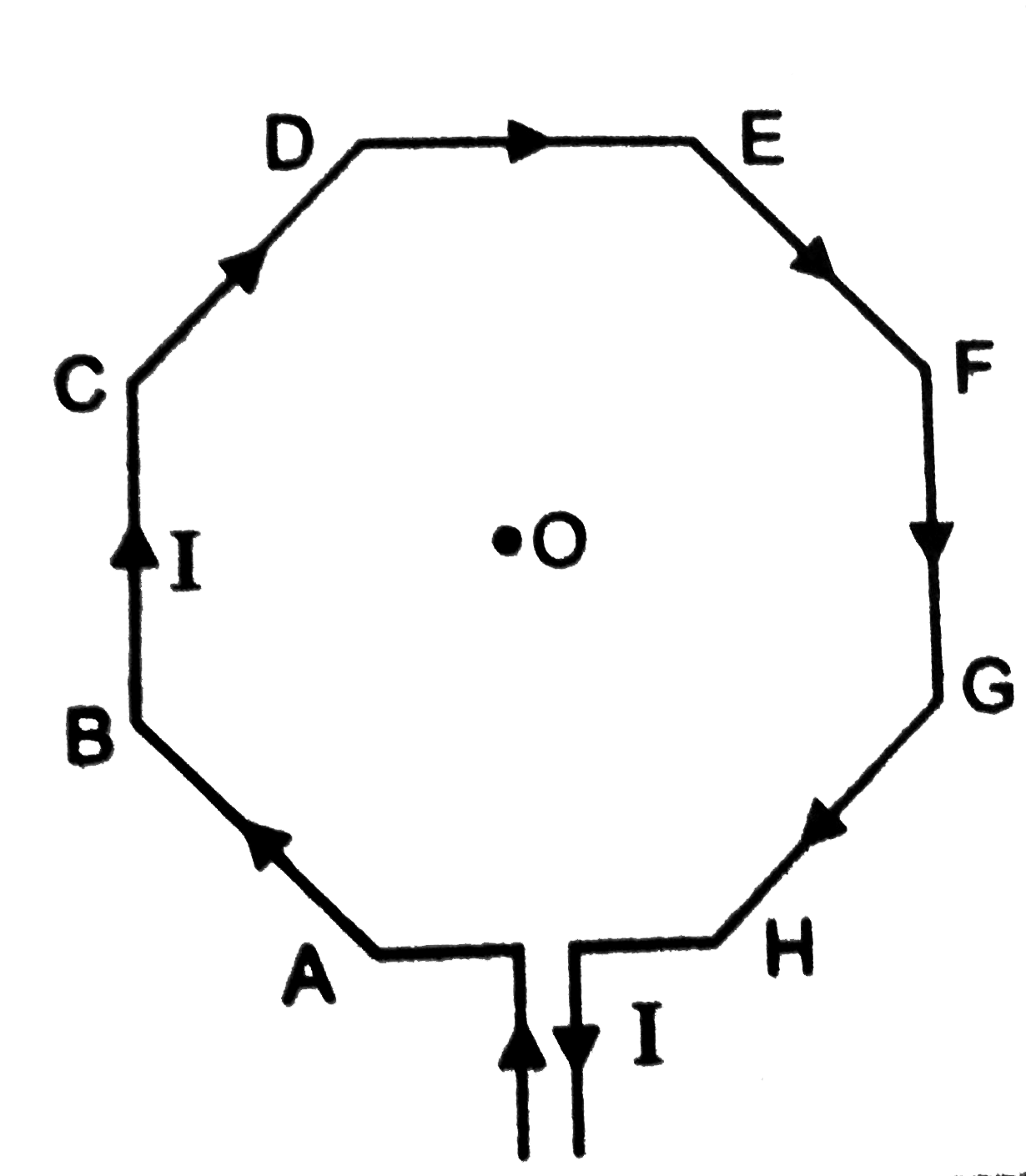 A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πa
A√5μ0I2πaBμ0I√5πaC5√2μ0IπaD5μ0I4πaDue to the flow of current in a circular loop of radius R, the magnetic induction produced at the centre of the loop is B. The magnetic moment of the loop is (μ0=permeability constant)
ABR3/2πμ0B2πBR3/μ0CBR2/2πμ0D2πBR2/μ0
A current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be

View SolutionThe magnetic induction at the centre of a current carrying circular of coil radius r, is
View SolutionIf the current flowing in a circular loop is in clockwise directions, then the magnetic induction will be
View SolutionIf the current flowing in a circular loop is in anticlockwise direction then the magnetic induction will be
View SolutionA current I flows through a closed loop as shown in figure. The magnetic field induction at the centre 0 is

View Solution
