An oil merchant has 3 varieties of oil of volumes 432, 594 and 702 respectively. The number of cans of equal size that would be required to fill the oil separately is:
किसी तेल व्यापारी के पास तीन किस्म के तेल की 432, 594 एवं 702 की मात्रा में हैं |तेल को अलग-अलग भरने के लिए आवश्यक बराबर आकार के पात्रों की संख्या ज्ञात करें |
13, 15, 17
8, 11, 13
8, 13, 15
6, 9, 11
To solve the problem of determining the number of cans of equal size required to fill the oil separately, we need to find the highest common factor (HCF) of the three volumes of oil: 432, 594, and 702. Here’s the step-by-step solution:
Step 1: Find the prime factorization of each volume.
For 432:
- Divide by 2: 432÷2=216
- Divide by 2: 216÷2=108
- Divide by 2: 108÷2=54
- Divide by 2: 54÷2=27
- Divide by 3: 27÷3=9
- Divide by 3: 9÷3=3
- Divide by 3: 3÷3=1
So, the prime factorization of 432 is:
432=24×33
For 594:
- Divide by 2: 594÷2=297
- Divide by 3: 297÷3=99
- Divide by 3: 99÷3=33
- Divide by 3: 33÷3=11
- Divide by 11: 11÷11=1
So, the prime factorization of 594 is:
594=21×33×111
For 702:
- Divide by 2: 702÷2=351
- Divide by 3: 351÷3=117
- Divide by 3: 117÷3=39
- Divide by 3: 39÷3=13
- Divide by 13: 13÷13=1
So, the prime factorization of 702 is:
702=21×33×131
Step 2: Identify the common factors.
Now, we will identify the common prime factors from the factorizations:
- For 2: The minimum power is 21 (from 594 and 702).
- For 3: The minimum power is 33 (common in all three).
- 11 and 13 are not common to all three.
Step 3: Calculate the HCF.
Thus, the HCF is:
HCF=21×33=2×27=54
Step 4: Calculate the number of cans required for each volume.
Now, we divide each volume by the HCF to find the number of cans:
- For 432:
Number of cans=43254=8
- For 594:
Number of cans=59454=11
- For 702:
Number of cans=70254=13
Final Answer:
The number of cans required to fill the oil separately are:
- 8 cans for 432
- 11 cans for 594
- 13 cans for 702
- Divide by 2: 432÷2=216
- Divide by 2: 216÷2=108
- Divide by 2: 108÷2=54
- Divide by 2: 54÷2=27
- Divide by 3: 27÷3=9
- Divide by 3: 9÷3=3
- Divide by 3: 3÷3=1
432=24×33
- Divide by 2: 594÷2=297
- Divide by 3: 297÷3=99
- Divide by 3: 99÷3=33
- Divide by 3: 33÷3=11
- Divide by 11: 11÷11=1
594=21×33×111
- Divide by 2: 702÷2=351
- Divide by 3: 351÷3=117
- Divide by 3: 117÷3=39
- Divide by 3: 39÷3=13
- Divide by 13: 13÷13=1
702=21×33×131
- For 2: The minimum power is 21 (from 594 and 702).
- For 3: The minimum power is 33 (common in all three).
- 11 and 13 are not common to all three.
HCF=21×33=2×27=54
Number of cans=43254=8
Number of cans=59454=11
Number of cans=70254=13
The number of cans required to fill the oil separately are:
- 8 cans for 432
- 11 cans for 594
- 13 cans for 702
Topper's Solved these Questions
Similar Questions
36 men and 48 women can do a certain work in one day whereas 6 men and 12 women can do it in 5 days. The number of women required to do the same work in 8 days is:
36 पुरुष और 48 महिलाएं एक दिन में एक काम को पूरा कर सकते हैं जबकि 6 पुरुष और 12 महिलाएं इसे 5 दिनों में पूरा कर सकते हैं। 8 दिनों में इस काम को करने के लिए आवश्यक महिलाओं की संख्या कितनी है?
View SolutionA milkman uses three containers for selling milk, their capacities being 40L, 30L and 20L respectively. He fills respectively 87.5%, 80% and 90% of the containers with a mix of milk and water in the ratios, 3:2, 5:1 and 7:2 respectively. What is the ratio of total quantity of milk to that of water carried by him ?
एक दूध वाला दूध बेचने के लिए तीन बर्तनों का इस्तेमाल करता है, उनकी धारिता क्रमशः 40 ली०, 30 ली० और 20 ली० है | वह बर्तनों का 87.5%, 80% और 90% भाग दूध और पानी से भरता है जो क्रमशः 3 : 2, 5 : 1 और 7 : 2 के अनुपात में हैं | उसके पास मौजूद दूध और पानी की कुल मात्रा का अनुपात ज्ञात करें |
View SolutionThe given Pie Chart (central angles are not as per any chosen scale) presents 116 percentage of the number of refrigerators of five different companies (with reference to the total number of refrigerators) in a hotel.
दिया गया पाई-चार्ट ( केंद्रीय कोण किसी भी चयनित पैमाने के अनुसार नहीं हैं ) किसी होटल में पांच अलग-अलग कंपनियों के रेफ्रिजिरेटरों की संख्या का प्रतिशत (रेफ्रिेजिरिटरों की कुल संख्या के संदर्भ में ) दर्शाता है |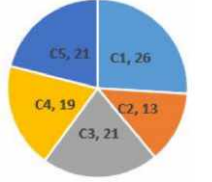 What is the difference in number of refrigerators supplied to the hotel by companies C1 and C5?
What is the difference in number of refrigerators supplied to the hotel by companies C1 and C5?
कंपनी C1 एवं C5 के द्वारा होटल को आपूर्ति किये गए रेफ्रिजिरेटरों की संख्या में क्या अंतर है ?
View SolutionThe given Pie Chart (central angles are not as per any chosen scale) presents 116 percentage of the number of refrigerators of five different companies (with reference to the total number of refrigerators) in a hotel.
दिया गया पाई-चार्ट ( केंद्रीय कोण किसी भी चयनित पैमाने के अनुसार नहीं हैं ) किसी होटल में पांच अलग-अलग कंपनियों के रेफ्रिजिरेटरों की संख्या का प्रतिशत (रेफ्रिेजिरिटरों की कुल संख्या के संदर्भ में ) दर्शाता है |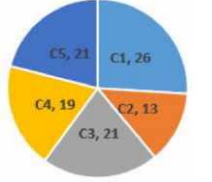 What is the difference between the central angles (to the nearest 0.1 degree) subtended by the
sectors for C2 and C4?
What is the difference between the central angles (to the nearest 0.1 degree) subtended by the
sectors for C2 and C4?
त्रिज्यखंडों के द्वारा C2 एवं C4 के लिए अंतरित केंद्रीय कोणों ( 0.1 डिग्री के निकटतम ) में क्या अंतर है
View SolutionThe price of cooking oil increased by 25%. Find by how much percentage a family must reduce its consumption in order to maintain the same budget? /
खाना पकाने के तेल की कीमत में 25% की वृद्धि हुई। उसी बजट को बनाए रखने के लिए एक परिवार को अपनी खपत में कितने प्रतिशत की कमी करनी चाहिए?
View SolutionThe given bar graph presents the number of different types of vehicles (in lakhs) exported by a company during 2014 and 2015.
दिया गया दंड आरेख एक कंपनी के द्वारा 2014 और 2015 में निर्यात किये गए अलग-अलग प्रकार के वाहनों की संख्या ( लाख में ) को दर्शाता है |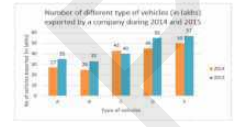 What is the ratio of the total number of type A and C vehicles exported in 2014 to the total number of type B and E vehicles exported in 2015?
What is the ratio of the total number of type A and C vehicles exported in 2014 to the total number of type B and E vehicles exported in 2015?
2014 में निर्यात किये गए A और C प्रकार के वाहनों की कुल संख्या का 2015 में निर्यात किये गए B एवं E प्रकार के वाहनों की कुल संख्या के साथ अनुपात ज्ञात करें |
View SolutionA and B can do a work in 15 days and 10 days respectively. They begin the work together but B leaves after two days. Now A completes the remaining work. The total number of days needed for the completion of the work is:
A और B क्रमशः 15 दिनों और 10 दिनों में एक कार्य कर सकते हैं। वे एक साथ कार्य शुरू करते हैं लेकिन B दो दिनों के बाद छोड़ देता हैं। अब A शेष कार्य को पूरा करता है। कार्य पूरा होने के लिए आवश्यक कुल दिनों की संख्या है:
View SolutionThree different positions of the same dice are shown. Find the number on the face opposite the face showing 3?
एक ही पासे की तीन अलग-अलग अवस्थाएं दी गयी हैं | 3 के विपरीत फलक पर मौजूद संख्या ज्ञात करें |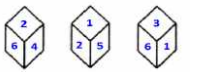
View SolutionThe table given below presents the number of books on different subjects kept on separate shelves. Subjects with odd and even numbers are of Arts and Science respectively.
नीचे दी गयी तालिका अलग-अलग विषयों की पुस्तकों की संख्या को दर्शाता है जिन्हें अलग-अलग खानों में रखा गया है | विषम तथा सम संख्या के विषय क्रमशः कला एवं विज्ञान हैं |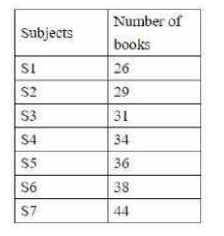 What is the ratio of the number of books of S1 and the average number of books per subject?
What is the ratio of the number of books of S1 and the average number of books per subject?
S1 के पुस्तकों की संख्या तथा प्रति विषय पुस्तकों की औसत संख्या में क्या अनुपात है ?
View SolutionThe table given below presents the number of books on different subjects kept on separate shelves. Subjects with odd and even numbers are of Arts and Science respectively.
नीचे दी गयी तालिका अलग-अलग विषयों की पुस्तकों की संख्या को दर्शाता है जिन्हें अलग-अलग खानों में रखा गया है | विषम तथा सम संख्या के विषय क्रमशः कला एवं विज्ञान हैं |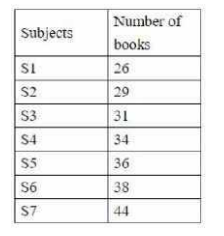 What is the ratio of the total number of books on Arts to that of Science?
What is the ratio of the total number of books on Arts to that of Science?
कला और विज्ञान की कुल पुस्तकों की संख्या में क्या अनुपात है ?
View Solution