Two small circular grounds of diameters 42 m and 26 m are to be replaced by a bigger circular ground. What would be the radius of the new ground if the new ground has the same area as the two small grounds?
42 मीटर और 26 मीटर व्यास के दो छोटे गोलाकार मैदानों को एक बड़े गोलाकार मैदान से बदलना है। यदि
नए मैदान का क्षेत्रफल, दो छोटे मैदानों के क्षेत्रफल के समान है, तो नई मैदान की त्रिज्या क्या होगी ?
24.69 m
23 m
25 m
25.01 m
To find the radius of the new circular ground that has the same area as the two smaller circular grounds, we can follow these steps:
Step 1: Calculate the radius of the two smaller circular grounds.
- The diameter of the first circular ground is 42 m, so its radius r1 is:
r1=422=21 m
- The diameter of the second circular ground is 26 m, so its radius r2 is:
r2=262=13 m
Step 2: Calculate the area of the two smaller circular grounds.
- The area A1 of the first circular ground is given by the formula A=πr2:
A1=π(21)2=π×441=441π m2
- The area A2 of the second circular ground is:
A2=π(13)2=π×169=169π m2
Step 3: Find the total area of the two smaller grounds.
- The total area Atotal is:
Atotal=A1+A2=441π+169π=610π m2
Step 4: Set the area of the new ground equal to the total area of the two smaller grounds.
- Let the radius of the new ground be R. The area of the new ground is:
Anew=πR2
- Setting this equal to the total area:
πR2=610π
Step 5: Solve for R.
- Dividing both sides by π:
R2=610
- Taking the square root of both sides:
R=√610≈24.7 m
Conclusion:
The radius of the new circular ground is approximately 24.7 meters.
---
- The diameter of the first circular ground is 42 m, so its radius r1 is:
r1=422=21 m
- The diameter of the second circular ground is 26 m, so its radius r2 is:
r2=262=13 m
- The area A1 of the first circular ground is given by the formula A=πr2:
A1=π(21)2=π×441=441π m2
- The area A2 of the second circular ground is:
A2=π(13)2=π×169=169π m2
- The total area Atotal is:
Atotal=A1+A2=441π+169π=610π m2
- Let the radius of the new ground be R. The area of the new ground is:
Anew=πR2
- Setting this equal to the total area:
πR2=610π
- Dividing both sides by π:
R2=610
- Taking the square root of both sides:
R=√610≈24.7 m
The radius of the new circular ground is approximately 24.7 meters.
Topper's Solved these Questions
Similar Questions
Two small circular plots of diameters 16 m and 12 m are to be replaced by a Bigger circular park. What would be the radius of this new park, if the new park has to occupy the same space as the two small parks? (a) 10 m (b) 15 m (c) 20 m (d) 25 m
View SolutionThe area of a circular playground is 22176 m2 .Find the cost of fencing this ground at the rate of Rs 50 per metre
View Solution
Knowledge Check
- Question 1 - Select One
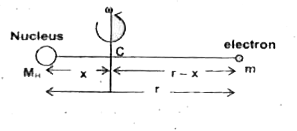
The new ground state energy of electron will beAmore than that found with Bohr atomBequal to energy found with Bohr atomCsmaller than energy found with Bohr atomDdata insufficient - Question 2 - Select One
A circular ground of radius 7 m is surrounded by a path of width 3.5 m. Find the area of the path (π=227)
A202 sq.mB154 sq.mC192.5sq.mD346 .5 sq. m
A man runs with a speed of 15.84 km/hr. He completes 12 rouds of a circular ground in one hour. Find the area of the ground
View SolutionThe area of a circular playground is 22176 m2 . Find the cost of fencing this ground at the rate of Rs. 50 per m.
View SolutionThe area of a circular plavground is 88704m^(2). Find the cost of fencing this ground at the rate of 65 per metre
View SolutionThe area of circular play ground is 154m2. Find its circumference.
View SolutionA solid metallic sphere of radius 15cm melted and recast into spherical balls of radius 3 cm each. What is the ratio of the surface area of the original and the sum of the surface area of the balls?
15 सेमी त्रिज्या का एक ठौस धात्विक क्षेत्र को पिघला कर त्रिज्या 3 सेमी के प्रत्येक गोलाकार गेंद बनाई जाती है । मूल सतह के क्षेत्रफल और गेंदों के सतह क्षेत्र के योग का अनुपात क्या है?View SolutionThe diameter of a roller is 2.4 m and its length is 1.68 m. If its rotates 1000 time to level a ground. Find the area of the ground.
View Solution

