In a circle with centre O, an arc ABC subtends an angle of 136∘ at the centre of the circle. Chord AB is produced to point P. Then ∠CBP is equal to :
केंद्र Oवाले एक वृत्त में, चाप ABC वृत्त के केंद्र पर 136∘ का कोण अंतरित करता है | जीवा AB को बिंदु P तक बढ़ाया जाता है | तो ∠CBP
का मान क्या होगा ?
72∘
44∘
68∘
66∘
To find the value of angle CBP in the given circle, we will follow these steps:
Step 1: Understand the given information
We have a circle with center O, and an arc ABC that subtends an angle of 136° at the center O. We need to find the angle CBP when chord AB is extended to point P.
Step 2: Use the property of angles subtended by an arc
According to the property of circles, the angle subtended at the center (angle AOC) is twice the angle subtended at any point on the circumference (angle ABC). Therefore, we can set up the equation:
∠AOC=2×∠ABC
Given that ∠AOC=136∘, we can find ∠ABC:
∠ABC=136∘2=68∘
Step 3: Identify the cyclic quadrilateral
Since points A, B, C, and P are on the circle, quadrilateral ABCP is cyclic. In a cyclic quadrilateral, the sum of the opposite angles is 180°:
∠ABC+∠ACP=180∘
Thus,
∠ACP=180∘−∠ABC=180∘−68∘=112∘
Step 4: Use the linear pair property
Now, since AB is extended to point P, angles ABC and CBP form a linear pair. Therefore, we can write:
∠ABC+∠CBP=180∘
Substituting the value of ∠ABC:
68∘+∠CBP=180∘
Now, we can solve for ∠CBP:
∠CBP=180∘−68∘=112∘
Conclusion
Thus, the value of angle CBP is:
∠CBP=112∘
We have a circle with center O, and an arc ABC that subtends an angle of 136° at the center O. We need to find the angle CBP when chord AB is extended to point P.
According to the property of circles, the angle subtended at the center (angle AOC) is twice the angle subtended at any point on the circumference (angle ABC). Therefore, we can set up the equation:
∠AOC=2×∠ABC
Given that ∠AOC=136∘, we can find ∠ABC:
∠ABC=136∘2=68∘
Since points A, B, C, and P are on the circle, quadrilateral ABCP is cyclic. In a cyclic quadrilateral, the sum of the opposite angles is 180°:
∠ABC+∠ACP=180∘
Thus,
∠ACP=180∘−∠ABC=180∘−68∘=112∘
Now, since AB is extended to point P, angles ABC and CBP form a linear pair. Therefore, we can write:
∠ABC+∠CBP=180∘
Substituting the value of ∠ABC:
68∘+∠CBP=180∘
Now, we can solve for ∠CBP:
∠CBP=180∘−68∘=112∘
Thus, the value of angle CBP is:
∠CBP=112∘
Topper's Solved these Questions
Similar Questions
In a circle with centre O, an arc ABC subtends an angle of 132∘ at the centre of the circle. Chord AB is produced to point P. Then ∠CBP is equal to :
केंद्र Oवाले एक वृत्त में, चाप ABC वृत्त के केंद्र पर 132∘ का कोण अंतरित करता है | जीवा AB को बिंदु P तक बढ़ाया जाता है | तो ∠CBP का मान क्या होगा ?
View SolutionIn a circle with centre O, an arc ABC subtends an angle of 140∘ at the centre of the circle. Chord AB is produced to point P. Then ∠CBP is equal to :
केंद्र Oवाले एक वृत्त में, चाप ABC वृत्त के केंद्र पर 140∘ का कोण अंतरित करता है | जीवा AB को बिंदु P तक बढ़ाया जाता है | तो ∠CBP का मान क्या होगा ?
View Solution
Knowledge Check
In a circle with centre O. an arc ABC subtends an angle of 136∘ at the centre of the circle. The chord AB is produced to a point P. Then ∠CBP is equal to :
A72∘B44∘C68∘D66∘In a circle with centre O an are ABC subtends an angle of 140∘ at the centre of the circle . The chord AB is produced to point P. Then ∠CBP is equal to :
A50∘B40∘C80∘D70∘In the given figure, O is the centre of a circle and arc ABC subtends an angle of 130∘ at O. AB is extended to P, Then, ∠PBC is equal to
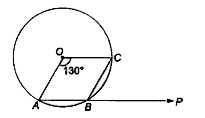 A25∘B40∘C65∘D75∘
A25∘B40∘C65∘D75∘
In a circle with centre O, an arc ABC subtends an angle of 110∘ at the centre of the circle. Chord AB is produced to point P. Then ∠CBP is equal to :
केंद्र Oवाले एक वृत्त में, चाप ABC वृत्त के केंद्र पर 110∘ का कोण अंतरित करता है | जीवा AB को बिंदु P तक बढ़ाया जाता है | तो ∠CBP का मान ज्ञात करें |
View SolutionPA and PB are two tangents to a circle with centre O, from P outside the circle. A and B are points on the circle. If ∠APB=100∘, then ∠OAB is equal to :
केंद्र O वाले एक वृत्त के बाहर किसी बिंदु P से खींची गई दो स्पर्श रेखाएँ PA और PB हैं | वृत्त पर A और B बिंदु हैं | यदि ∠APB=100∘,तो ∠OAB का क्या होगा ?
View SolutionIn a circle with centre O, a diameter AB is produced to a point P lying outside the circle and PT is a tangent to the circle at the point C on it, If ∠BPT=36∘, then what is the measure of ∠BCP ?
O केंद्र वाले एक वृत्त में, एक व्यास AB को वृत्त के बाहर स्थित एक बिंदु P तक बढ़ाया जाता है और PT उस बिंदु C पर वृत्त के स्प्शरिखा है, यदि ∠BPT=36∘ है, तो ∠BCP का माप क्या है?
View SolutionPA and PB are two tangents from a point P outside a circle with centre O. If A and B are points on the circle such that ∠APB=80∘, then ∠OAB is equal to:
PA और PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे दो बिंदु हैं कि ∠APB=80∘ है, तो ∠OAB का मान क्या होगा ?
View SolutionIn a circle with centre O, ABDC is a cyclic quadrilateral with AB as a diameter of the circle. AC and BD produced meet at E. If ∠CED=70∘, then what is the measure of ∠COD?
केंद्र O वाले एक वृत्त में, ABDC एक चक्रीय चतुर्भुज है जिसमें AB वृत्त का व्यास है| AC और BD को बढ़ाया गया है जो E पर मिलते हैं | यदि ∠CED=70∘ है, तो ∠COD का मान ज्ञात करें |
View Solution
