The sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBD and ∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is :
एक त्रिभुज ABC की भुजाएं AB और AC को क्रमशः बिंदु D तथा E तक बढ़ाया जाता है | ∠CBD तथा ∠BCE के समद्विभाजक P पर मिलते हैं | यदि ∠A=72∘ है, तो कोण P का मान ज्ञात करें
36∘
45∘
60∘
54∘
To solve the problem, we need to find the measure of angle P, which is formed by the bisectors of angles CBD and BCE in triangle ABC, where angle A is given as 72°.
1. Identify the angles in triangle ABC:
- Given that angle A = 72°.
- Let angle B = x and angle C = y.
2. Use the triangle angle sum property:
- The sum of angles in a triangle is 180°.
- Therefore, we have:
A+B+C=180°
Substituting the known value:
72°+x+y=180°
Simplifying gives:
x+y=108°
3. Identify angles CBD and BCE:
- Angle CBD is formed by extending side AB to point D, and angle BCE is formed by extending side AC to point E.
- Therefore, we can express these angles as:
∠CBD=180°−y(since it is exterior to triangle ABC)
∠BCE=180°−x(since it is exterior to triangle ABC)
4. Find the measures of angles CBD and BCE:
- Substitute the expressions for x and y:
∠CBD=180°−y=180°−(108°−x)=72°+x
∠BCE=180°−x=180°−x
5. Use the angle bisector theorem:
- The angle bisector of angle CBD and angle BCE meets at point P.
- The measure of angle P can be calculated using the formula:
∠P=90°−A2
- Substituting the value of angle A:
∠P=90°−72°2=90°−36°=54°
Conclusion:
The measure of angle P is 54°.
- Given that angle A = 72°.
- Let angle B = x and angle C = y.
- The sum of angles in a triangle is 180°.
- Therefore, we have:
A+B+C=180°
Substituting the known value:
72°+x+y=180°
Simplifying gives:
x+y=108°
- Angle CBD is formed by extending side AB to point D, and angle BCE is formed by extending side AC to point E.
- Therefore, we can express these angles as:
∠CBD=180°−y(since it is exterior to triangle ABC)
∠BCE=180°−x(since it is exterior to triangle ABC)
- Substitute the expressions for x and y:
∠CBD=180°−y=180°−(108°−x)=72°+x
∠BCE=180°−x=180°−x
- The angle bisector of angle CBD and angle BCE meets at point P.
- The measure of angle P can be calculated using the formula:
∠P=90°−A2
- Substituting the value of angle A:
∠P=90°−72°2=90°−36°=54°
The measure of angle P is 54°.
Topper's Solved these Questions
Similar Questions
The sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBDand∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is:
View SolutionThe sides PQ and PR of △PQR are produced to points S and T, respectively. The bisectors of ∠SQR and ∠TRQ meet at U. If ∠QUR=79∘ , then the measure of ∠P is:
त्रिभुज PQR की भुजाओ PQ और QR को क्रमशः S और T तक बढ़ाया जाता है| ∠SQR और ∠TRQ के समद्विभाजक U पर मिलते हैं| यदि ∠QUR=79∘ है, तो कोण P का मान ज्ञात करें |
View Solution
Knowledge Check
The sides AB and AC of △ABC are produced to points D and E, respectiely. The bisectors of ∠CBD and ∠BCE meet at P. If ∠A=82∘, then the measure of ∠P is :
A54∘B60∘C36∘D49∘In figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
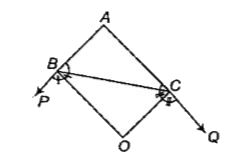 A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
The sides AB and AC of △ABC are produced to P and Q respectively. The bisectors of ∠CBP and ∠BCQ meet at O. If the measure of ∠A is 44∘, then what is the measure of 12∠BOC?
एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P और Q तक बढ़ाया जाता है | ∠CBP और ∠BCQ के समद्विभाजक O पर मिलते हैं| यदि कोण A का मान 44∘ है, तो 12∠BOC का मान क्या होगा ?
View SolutionIn a △ABC, the sides AB and AC are extended to P and Q respectively. The bisectors of ∠PBC and ∠QCB intersect at a point R. If ∠R=66∘, then the measure of ∠A is :
त्रिभुज ABC में, AB और AC भुजाओं को क्रमशः P और Q तक बढ़ाया जाता है| ∠PBC तथा ∠QCB के द्विभाजक एक बिंदु R पर मिलते हैं | यदि ∠R=66∘, है, तो कोण A का मान ज्ञात करें |
View SolutionThe sides PQ and PR od △PQR are produced to point S and T, respectively. The bisector of ∠SQR and ∠TRQ, meet at U. If ∠QUR=59∘, then the measure of ∠P is:
△PQR की भुजाएँ PQ और PR क्रमशः बिंदु S और T तक बढ़ाया जाता हैं।∠SQR और ∠TRQ के द्विभाजक, U पर मिलते हैं। यदि ∠QUR=59∘ है, तो ∠P का माप है :
View SolutionThe sides AB and AC of a △ABC are extended to P and Q respectively. If the bisectors of ∠PBC and ∠QCB intersect at O, and ∠A=92∘, then ∠BOC is equal to:
एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P तथा Q तक बढ़ाया जाता है | यदि ∠PBC तथा ∠QCB के समद्विभाजक एक दूसरे को O पर काटते हैं तथा ∠A=92∘ है, तो ∠BOC किसके बराबर है ?
View SolutionIn △ABC ,∠B=68∘ and ∠C=32∘ . Sides AB and AC are produced to points D and E, respectively. The bisectors of ∠DBC and ∠BCE meet at F. What is the measure of ∠BFC ? /
△ABC में, ∠B=68∘ तथा ∠C=32∘ है | भुजाओं AB और AC को क्रमशः बिंदु D और E तक बढ़ाया जाता है | ∠DBC तथा ∠BCE के समद्विभाजक F पर मिलते हैं | कोण BFC का मान ज्ञात करें |
View SolutionThe sides AB and AC of △ABC are produced to P and Q respectively. The bisectors of ∠CBP and ∠BCQ meet at R. If the measure of ∠A is 44∘, then what is the measure of 12∠BRC?
त्रिभुज ABC की AB और AC भुजाएं क्रमशः P और Q बनाती हैं। ∠CBP और ∠BCQ के द्विभाजक R पर मिलते हैं। अगर ∠A का माप 44∘ है तो 12∠BRC का माप क्या है?
View Solution
