In ,. Its sides AB and AC are produced to the point D and E. If the bisectors of the and meet at the point O, then will be equal to:
त्रिभुज ABC में, है | इसकी
भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो का मान किसके बराबर होगा ?
To solve the problem, we need to find the angle ∠BOC in triangle ABC where ∠A=50∘ and the sides AB and AC are extended to points D and E respectively. The angle bisectors of ∠CBD and ∠BCE meet at point O.
1. Identify the angles in triangle ABC:
- Given ∠A=50∘.
- By the triangle angle sum property, we know that ∠A+∠B+∠C=180∘.
- Let ∠B=b and ∠C=c.
- Therefore, b+c=180∘−50∘=130∘.
2. Determine angles CBD and BCE:
- When we extend sides AB and AC to points D and E, we can express the angles ∠CBD and ∠BCE.
- The angle ∠CBD is equal to ∠B+∠A (exterior angle theorem).
- Thus, ∠CBD=b+50∘.
- Similarly, ∠BCE=∠C+∠A=c+50∘.
3. Calculate the angle bisectors:
- The angle bisector of ∠CBD divides it into two equal parts:
∠OBD=b+50∘2
- The angle bisector of ∠BCE divides it into two equal parts:
∠OCE=c+50∘2
4. Find angle BOC:
- The angle ∠BOC can be calculated using the fact that:
∠BOC=180∘−(∠OBD+∠OCE)
- Substitute the values:
∠BOC=180∘−(b+50∘2+c+50∘2)
- Combine the terms:
∠BOC=180∘−(b+c+100∘2)
- Since b+c=130∘:
∠BOC=180∘−(130∘+100∘2)
∠BOC=180∘−(230∘2)
∠BOC=180∘−115∘=65∘
Final Answer:
∠BOC=65∘
- Given ∠A=50∘.
- By the triangle angle sum property, we know that ∠A+∠B+∠C=180∘.
- Let ∠B=b and ∠C=c.
- Therefore, b+c=180∘−50∘=130∘.
- When we extend sides AB and AC to points D and E, we can express the angles ∠CBD and ∠BCE.
- The angle ∠CBD is equal to ∠B+∠A (exterior angle theorem).
- Thus, ∠CBD=b+50∘.
- Similarly, ∠BCE=∠C+∠A=c+50∘.
- The angle bisector of ∠CBD divides it into two equal parts:
∠OBD=b+50∘2
- The angle bisector of ∠BCE divides it into two equal parts:
∠OCE=c+50∘2
- The angle ∠BOC can be calculated using the fact that:
∠BOC=180∘−(∠OBD+∠OCE)
- Substitute the values:
∠BOC=180∘−(b+50∘2+c+50∘2)
- Combine the terms:
∠BOC=180∘−(b+c+100∘2)
- Since b+c=130∘:
∠BOC=180∘−(130∘+100∘2)
∠BOC=180∘−(230∘2)
∠BOC=180∘−115∘=65∘
∠BOC=65∘
Topper's Solved these Questions
Similar Questions
In △ABC ,∠A=50∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=50∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान क्या होगा ?
View SolutionIn △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View Solution
Knowledge Check
In △ABC ,∠A=50∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=50∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान क्या होगा ?A70∘B65∘C55∘D40∘In figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
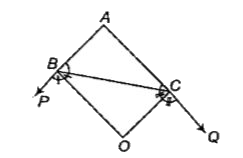 A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
In △ABC ,∠A=70∘. AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=70∘ में AB और AC को क्रमशः बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान क्या होगा ?
View SolutionIn △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View SolutionIn a △ABC, ∠A=52∘. Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBD and ∠BCE meet at point O, then ∠BOC is equal to:
△ABC में ∠A=52∘ है। इनकी भुजाएं AB और AC क्रमशः D और E तक बढाई जाती है। अगर ∠CBD और ∠BCE समदूविभाजक बिंदु O पर मिलते हैं, तो ∠BOC बराबर हैः
View SolutionIn △ABC ,∠A=66∘. AB and AC are produced to points D and E respectively. If the bisector of angle ∠CBD and ∠BCE meet at the point O, then ∠BOC is equal to :
त्रिभुज ABC में, ∠A=66∘ ,AB और AC क्रमशः D और E तक बढ़ाये जाते हैं। यदि कोण ∠CBD और ∠BCE के सम द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC के ज्ञात करे
View SolutionIn ∠ABC, AB and AC are produced to points D and E respectively. If the bisector of ∠CBD and ∠BCE meet at a point O and ∠BOC=57∘, then ∠A is equal to :
त्रिभुज ABC में, AB और AC क्रमशः D और E तक बढ़ाये जाते हैं। यदि कोण ∠CBD और ∠BCE के सम द्विभाजक बिंदु O पर मिलते हैं, और ∠BOC=57∘ तो ∠A बराबर है
View SolutionIn △ABC ,∠B=68∘ and ∠C=32∘ . Sides AB and AC are produced to points D and E, respectively. The bisectors of ∠DBC and ∠BCE meet at F. What is the measure of ∠BFC ? /
△ABC में, ∠B=68∘ तथा ∠C=32∘ है | भुजाओं AB और AC को क्रमशः बिंदु D और E तक बढ़ाया जाता है | ∠DBC तथा ∠BCE के समद्विभाजक F पर मिलते हैं | कोण BFC का मान ज्ञात करें |
View Solution
