In a △ABC, ∠A=52∘. Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBD and ∠BCE meet at point O, then ∠BOC is equal to:
△ABC में ∠A=52∘ है। इनकी भुजाएं AB और AC क्रमशः D और E तक बढाई जाती है। अगर ∠CBD और ∠BCE समदूविभाजक बिंदु O पर मिलते हैं, तो ∠BOC बराबर हैः
16∘
106∘
32∘
64∘
To solve the problem step by step, we will analyze the triangle ABC and the angles involved.
Step 1: Understand the Triangle and Given Angles
We have triangle ABC with angle A = 52°. We need to find angle BOC where O is the intersection of the angle bisectors of angles CBD and BCE.
Hint: Remember that the sum of angles in a triangle is 180°.
Step 2: Extend the Sides of the Triangle
Extend side AB to point D and side AC to point E. This creates two new angles: angle CBD and angle BCE.
Hint: Visualizing the triangle and its extensions can help in understanding the relationships between the angles.
Step 3: Identify the Angles Involved
From triangle ABC, we know:
- Angle A = 52°
- Let angle B = x
- Let angle C = y
Using the triangle angle sum property:
x+y+52°=180°
Thus,
x+y=128°
Hint: Use the triangle sum property to express the unknown angles in terms of known angles.
Step 4: Use the Angle Bisector Theorem
The angle bisector of angle CBD will create two angles:
- Angle OBD = x/2
- Angle OBC = y/2
Similarly, the angle bisector of angle BCE will create:
- Angle OCE = y/2
- Angle OCB = x/2
Hint: Remember that the angle bisector divides the angle into two equal parts.
Step 5: Calculate Angle BOC
The angle BOC can be calculated using the external angle bisector theorem:
Angle BOC=180°−(x2+y2)
Substituting x+y=128°:
Angle BOC=180°−(128°2)
Angle BOC=180°−64°
Angle BOC=116°
However, we need to consider the angles formed by the extensions, which gives:
Angle BOC=180°−116°=64°
Hint: Be careful with the signs when calculating angles formed by external bisectors.
Conclusion
Thus, angle BOC is equal to 64°.
Final Answer
The correct option is 4th option: 64°.
We have triangle ABC with angle A = 52°. We need to find angle BOC where O is the intersection of the angle bisectors of angles CBD and BCE.
Extend side AB to point D and side AC to point E. This creates two new angles: angle CBD and angle BCE.
From triangle ABC, we know:
- Angle A = 52°
- Let angle B = x
- Let angle C = y
x+y+52°=180°
Thus,
x+y=128°
The angle bisector of angle CBD will create two angles:
- Angle OBD = x/2
- Angle OBC = y/2
- Angle OCE = y/2
- Angle OCB = x/2
The angle BOC can be calculated using the external angle bisector theorem:
Angle BOC=180°−(x2+y2)
Angle BOC=180°−(128°2)
Angle BOC=180°−64°
Angle BOC=116°
Angle BOC=180°−116°=64°
Thus, angle BOC is equal to 64°.
The correct option is 4th option: 64°.
Similar Questions
In △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View SolutionIn △ABC ,∠A=66∘. AB and AC are produced to points D and E respectively. If the bisector of angle ∠CBD and ∠BCE meet at the point O, then ∠BOC is equal to :
त्रिभुज ABC में, ∠A=66∘ ,AB और AC क्रमशः D और E तक बढ़ाये जाते हैं। यदि कोण ∠CBD और ∠BCE के सम द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC के ज्ञात करे
View Solution
Knowledge Check
In figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
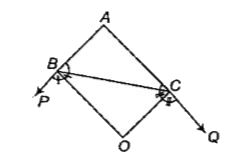 A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the aboveIn △ABC ,∠A=50∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=50∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान क्या होगा ?A70∘B65∘C55∘D40∘
In △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View SolutionIn △ABC ,∠A=50∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=50∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान क्या होगा ?
View SolutionIn △ABC ,∠A=50∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=50∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान किसके बराबर होगा ?
View SolutionIn ∠ABC, AB and AC are produced to points D and E respectively. If the bisector of ∠CBD and ∠BCE meet at a point O and ∠BOC=57∘, then ∠A is equal to :
त्रिभुज ABC में, AB और AC क्रमशः D और E तक बढ़ाये जाते हैं। यदि कोण ∠CBD और ∠BCE के सम द्विभाजक बिंदु O पर मिलते हैं, और ∠BOC=57∘ तो ∠A बराबर है
View SolutionIn △ABC ,∠A=70∘. AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=70∘ में AB और AC को क्रमशः बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान क्या होगा ?
View SolutionThe sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBDand∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is:
View Solution
